题目内容
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)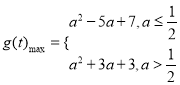
【解析】
试题(1)设二次函数一般式,根据待定系数法求出a,b,c(2)不等式恒成立一般转化为对应函数最值:x2-3x+1的最小值>m,再根据二次函数性质求x2-3x+1的最小值得实数m的范围;(3)根据对称轴与定义区间位置关系,分类讨论函数取最大值的情况
试题解析:解:(1)令f(x)=ax2+bx+c(a≠0),代入已知条件,
得:![]()
∴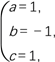
∴f(x)=x2-x+1.
(2)当x∈[-1,1]时,f(x)>2x+m恒成立,
即x2-3x+1>m恒成立;
令g(x)=x2-3x+1=![]() 2-
2-![]() ,x∈[-1,1].
,x∈[-1,1].
则对称轴:x=![]() [-1,1],g(x)min=g(1)=-1,
[-1,1],g(x)min=g(1)=-1,
∴m<-1.
(3)G(t)=f(2t+a)=4t2+(4a-2)t+a2-a+1,t∈[-1,1],对称轴为:t=![]() .
.
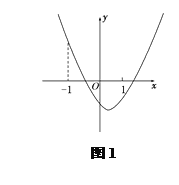
①当![]() ≥0时,即:a≤
≥0时,即:a≤![]() ;如图1:
;如图1:
G(t)max=G(-1)=4-(4a-2)+a2-a+1=a2-5a+7,
②当![]() <0时,
<0时,
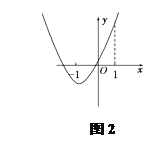 即:a>
即:a>![]() ;如图2:
;如图2:
G(t)max=G(1)=4+(4a-2)+a2-a+1=a2+3a+3,
综上所述:
G(t)max=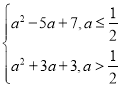

练习册系列答案
相关题目
