Question

5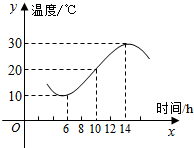．如图，某地一天从6时到14时的温度变化曲线近似满足函数f（x）=Asin（ωx+φ）+b，（A＞0，ω＞0，0＜φ＜π）．
（1）写出这段曲线的函数f（x）的解析式；
（2）当x∈R时，若函数g（x）=f（x+m）是偶函数，求实数|m|的最小值．

Answer 1

分析 （1）由图可知$\frac{1}{2}•\frac{2π}{ω}$=14-6，解得ω，由图示A=$\frac{1}{2}$（30-10）=10，b=$\frac{1}{2}$（30+10）=20，将x=6，y=10代入上式可取φ=$\frac{3π}{4}$，即可得解．
（2）先求得g（x）=f（x+m）=10sin（$\frac{π}{8}$x+$\frac{mπ}{8}$+$\frac{3π}{4}$）+20，x∈R，由g（x）=f（x+m）是偶函数可得g（x）=g（-x），对x∈R恒成立，即sin$\frac{π}{8}$x•cos（$\frac{mπ}{8}$+$\frac{3π}{4}$）=0对x∈R恒成立，可得cos（$\frac{mπ}{8}$+$\frac{3π}{4}$）=0，即可得解．

解答 本小题满分（12分）
解：（1）图中从6时到14时的图象是函数y=Asin（ωx+φ）+b的半个周期的图象．
∴$\frac{1}{2}•\frac{2π}{ω}$=14-6，解得ω=$\frac{π}{8}$．------------------------------------------（2分）
由图示A=$\frac{1}{2}$（30-10）=10，b=$\frac{1}{2}$（30+10）=20-------------------------------（4分）
∴y=10sin（$\frac{π}{8}$x+φ）+20
将x=6，y=10代入上式可取φ=$\frac{3π}{4}$---------------------------------------（6分）
故所求的解析式为y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20，x∈[6，14]---------------------（7分）
（2）易得g（x）=f（x+m）=10sin（$\frac{π}{8}$x+$\frac{mπ}{8}$+$\frac{3π}{4}$）+20，x∈R----------------（8分）
由g（x）=f（x+m）是偶函数可得，
∴g（x）=g（-x），对x∈R恒成立，
也即sin（$\frac{π}{8}$x+$\frac{mπ}{8}$+$\frac{3π}{4}$）=sin（-$\frac{π}{8}$x+$\frac{mπ}{8}$+$\frac{3π}{4}$）对x∈R恒成立
即sin$\frac{π}{8}$x•cos（$\frac{mπ}{8}$+$\frac{3π}{4}$）=0对x∈R恒成立----------------------------（10分）
∴cos（$\frac{mπ}{8}$+$\frac{3π}{4}$）=0，
∴$\frac{mπ}{8}$+$\frac{3π}{4}$=kπ+$\frac{π}{2}$，k∈Z，
∴m=8k-2，k∈Z，------------------------------------------------（11分）
所以实数|m|的最小值为2-------------------------------------------（12分）

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，正弦函数的图象和性质，属于基本知识的考查．