题目内容
17.已知数列{an}的前n项和为Sn,其中a1=1,an+1=2Sn+1(n∈N*),若数列{bn}满足:bn=log3an.(1)求数列{bn}的通项公式;
(2)令cn=$\frac{1}{{b}_{n+1}{b}_{n+3}}$,求数列{cn}的前n项和Tn.
分析 (1)通过an+1=2Sn+1与an+2=2Sn+1+1作差、整理得an+2=3an+1,进而an=3n-1,从而利用对数的性质可知bn=n-1;
(2)通过(1)、裂项可知cn=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),进而并项相加即得结论.
解答 解:(1)∵an+1=2Sn+1,
∴an+2=2Sn+1+1,
两式相减得:an+2-an+1=2Sn+1+1-(2Sn+1)=2an+1,
∴an+2=3an+1,
又∵a2=2S1+1=3=3a1满足上式,
∴数列{an}是以1为首项、3为公比的等比数列,
∴an=3n-1,
∴bn=log3an=log33n-1=n-1,
∴数列{bn}的通项公式bn=n-1;
(2)由(1)可知cn=$\frac{1}{{b}_{n+1}{b}_{n+3}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$).
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
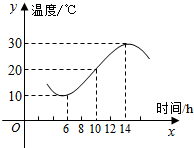 如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).
如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).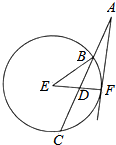 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$. 一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.
一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.