题目内容
20.设直角三角形中两锐角为A和B,则cosAcosB的取值范围是( )| A. | (0,$\frac{1}{2}$] | B. | (0,1) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{\sqrt{3}}{4}$,1) |
分析 利用积化和差公式化简所给的式子,再利用余弦函数的定义域和值域,求得该式子的范围.
解答 解:直角三角形中两锐角为A和B,A+B=C=$\frac{π}{2}$,
则cosAcosB=$\frac{1}{2}$[cos(A-B)+cos(A+B)]=$\frac{1}{2}$cos(A-B),
再结合A-B∈(-$\frac{π}{2}$,$\frac{π}{2}$),
可得cos(A-B)∈(0,1],
∴$\frac{1}{2}$cos(A-B)∈(0,$\frac{1}{2}$],
故选:A.
点评 本题主要考查积化和差公式的应用,余弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
10.已知点P(tanα,cosα)在第三象限,则角α的终边在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
15.已知定义在(0,+∞)上的单调函数f(x),对?x∈(0,+∞),都有f[f(x)-log2x]=3,则方程f(x)-f′(x)=2的解所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (2,3) |
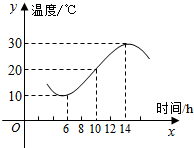 如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).
如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).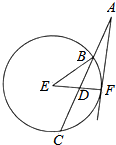 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$. 一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.
一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.