题目内容
15.已知函数f(x)=lnx-$\frac{1}{2}$ax2-2x的单调递减区间为(m,m+2),则a的值为$\frac{1-\sqrt{5}}{2}$.分析 先求出函数f(x)的导数,得到m,m+2是方程ax2+2x-1=0的2个根,根据方程根与系数的关系,解关于a的方程即可.
解答 解:f′(x)=$\frac{1}{x}$-ax-2=$\frac{1-{ax}^{2}-2x}{x}$,
由题意知f′(x)<0有实数解,
∵x>0,∴m>0.m+2>0,
由m+m+2=-$\frac{2}{a}$,m•(m+2)=-$\frac{1}{a}$,
得;a<0
当a<0时,只要△=4+4a>0,
∴-1<a<0,
由题意得:m,m+2是方程ax2+2x-1=0的2个根,
由m+m+2=-$\frac{2}{a}$,m•(m+2)=-$\frac{1}{a}$,
得:|m+2-m|=$\sqrt{{(-\frac{2}{a})}^{2}-4•(-\frac{1}{a})}$=2,
∴a2-2a-4=0,
解得:a=$\frac{1±\sqrt{5}}{2}$,∵-1<a<0,
故答案为:$\frac{1-\sqrt{5}}{2}$.
点评 本题考查了导数的应用,考查韦达定理,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:
由表中数据直观分析,收看新闻节目的观众是否与年龄有关是(填“是”或“否”)
| 文艺节目 | 新闻节目 | 总计 | |
| 20岁至40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
10.已知点P(tanα,cosα)在第三象限,则角α的终边在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
4.将y=sin(2x-$\frac{π}{6}$)图象向右平移$\frac{π}{12}$个单位,所得函数图象的一条对称轴的方程是( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=-$\frac{π}{12}$ |

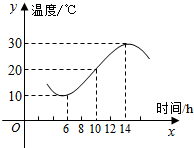 如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).
如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).