��Ŀ����
9������֪����x�IJ���ʽax2+bx+c��0�Ľ⼯Ϊ��1��2���������x�IJ���ʽcx2+bx+a��0�����������µ�һ�ֽⷨ���⣺��ax2+bx+c��0�Ľ⼯Ϊ��1��2�����ã�a��$\frac{1}{x}$��2+b��$\frac{1}{x}$��+c��0�Ľ⼯Ϊ��$\frac{1}{2}$��1����
������x�IJ���ʽcx2+bx+a��0�Ľ⼯Ϊ��$\frac{1}{2}$��1����
�ο������ⷨ��������x�IJ���ʽ$\frac{b}{x+a}$+$\frac{x+b}{x+c}$��0�Ľ⼯Ϊ��-1��-$\frac{1}{3}$���ȣ�$\frac{1}{2}$��1���������x�IJ���ʽ$\frac{b}{x-a}$-$\frac{x-b}{x-c}$��0�Ľ⼯Ϊ��������
| A�� | ��-1��1�� | B�� | ��-1��-$\frac{1}{2}$���ȣ�$\frac{1}{3}$��1�� | C�� | ��-�ޣ�-$\frac{1}{2}$���ȣ�$\frac{1}{3}$��1�� | D�� | ��-�ޣ�-$\frac{1}{2}$���ȣ�$\frac{1}{3}$��+�ޣ� |
���� ������Ŀ�еĽⷨ��д����Ӧ����ʽ�Ľ����̼��ɣ�
��� �⣺�������⣬
��$\frac{b}{x+a}$+$\frac{x+b}{x+c}$��0�Ľ⼯Ϊ��-1��-$\frac{1}{3}$���ȣ�$\frac{1}{2}$��1����
��$\frac{b}{-x+a}$+$\frac{-x+b}{-x+c}$��0�Ľ⼯Ϊ��-1��-$\frac{1}{2}$���ȣ�$\frac{1}{3}$��1����
��$\frac{b}{x-a}$-$\frac{x-b}{x-c}$��0�Ľ⼯Ϊ��-1��-$\frac{1}{2}$���ȣ�$\frac{1}{3}$��1����
��ѡ��B��
���� ���⿼���˲���ʽ�Ľⷨ��Ӧ�����⣬Ҳ�����˹�����̽�������⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
20�����к����У����䶨�����ڼ����溯���������������ǣ�������
| A�� | y=tanx | B�� | y=2x | C�� | y=x | D�� | y=lg��1+x2�� |
17����������y=sinx�ڵ㣨$\frac{��}{3}$��$\frac{\sqrt{3}}{2}$�������߷����ǣ�������
| A�� | x+2y-$\sqrt{3}$+$\frac{��}{3}$=0 | B�� | x-2y+$\sqrt{3}$-$\frac{��}{3}$=0 | C�� | $\sqrt{3}$x-2y+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$��=0 | D�� | $\sqrt{3}$x+2y-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$��=0 |
4��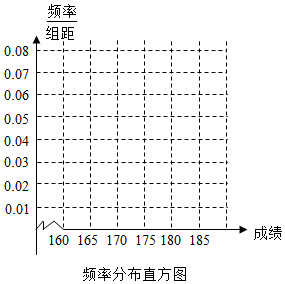 ij��У��2009��������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�����ͼ��ʾ��
ij��У��2009��������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�����ͼ��ʾ��
��1���������Ƶ�ʷֲ����Т١���λ����Ӧ���ݣ����ڴ���ֽ���������Ƶ�ʷֲ�ֱ��ͼ��
��2��Ϊ����ѡ�γ��������ѧ������У�����ڱ��Գɼ��ߵĵ�3��4��5�����÷ֲ������ȡ6��ѧ������ڶ������ԣ����3��4��5��ÿ�����ȡ������ѧ������ڶ������ԣ�
��3���ڣ�2����ǰ���£�ѧУ������6��ѧ���������ȡ2��ѧ������A���ٽ������ԣ���4��������һ��ѧ��������A���Եĸ��ʣ�
 ij��У��2009��������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�����ͼ��ʾ��
ij��У��2009��������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�����ͼ��ʾ����1���������Ƶ�ʷֲ����Т١���λ����Ӧ���ݣ����ڴ���ֽ���������Ƶ�ʷֲ�ֱ��ͼ��
��2��Ϊ����ѡ�γ��������ѧ������У�����ڱ��Գɼ��ߵĵ�3��4��5�����÷ֲ������ȡ6��ѧ������ڶ������ԣ����3��4��5��ÿ�����ȡ������ѧ������ڶ������ԣ�
��3���ڣ�2����ǰ���£�ѧУ������6��ѧ���������ȡ2��ѧ������A���ٽ������ԣ���4��������һ��ѧ��������A���Եĸ��ʣ�
| ��� | ���� | Ƶ�� | Ƶ�� |
| ��1�� | [160��165�� | 5 | 0.050 |
| ��2�� | [165��170�� | �� | 0.350 |
| ��3�� | [170��175�� | 30 | �� |
| ��4�� | [175��180�� | 20 | 0.200 |
| ��5�� | [180��185�� | 10 | 0.100 |
| �ϼ� | 100 | 1.00 | |
1�������x��y����Լ������$\left\{\begin{array}{l}{x-y��1}\\{x+y��1}\\{y-2��0}\end{array}\right.$����Ŀ�꺯��z=3x+y�����ֵΪ��������
| A�� | -1 | B�� | 3 | C�� | 11 | D�� | 12 |
18��5λ������5λŮ���ų�һ�ţ���������������֮������ֻ��2λŮ����Ů�����������ˣ���������������Ϊ��������
| A�� | 5760 | B�� | 57600 | C�� | 2880 | D�� | 28800 |
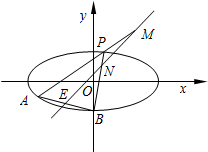 ��ͼ����֪��Բ$C��\frac{x^2}{12}+\frac{y^2}{4}=1$����B�����¶��㣬����B��ֱ�߽���ԲC����һ��A��A����x���·��������߶�AB���е�E��ֱ��y=x�ϣ�
��ͼ����֪��Բ$C��\frac{x^2}{12}+\frac{y^2}{4}=1$����B�����¶��㣬����B��ֱ�߽���ԲC����һ��A��A����x���·��������߶�AB���е�E��ֱ��y=x�ϣ�