题目内容
16.一个袋中装有5个形状大小完全相同的围棋子,其中3个黑子,2个白子.(Ⅰ)从袋中随机取出两个棋子,求取出的两个棋子颜色相同的概率;
(Ⅱ)从袋中随机取出一个棋子,将棋子放回后再从袋中随机取出一个棋子,求两次取出的棋子中至少有一个白子的概率.
分析 (Ⅰ)先计算从袋中随机取出两个棋子的情况总数,再求出取出的两个棋子颜色相同的情况总数,代入古典概型概率计算公式,可得答案.
(Ⅱ)先计算从袋中有放回的取出两个棋子的情况总数,再求出两次取出的棋子中至少有一个白子的情况总数,代入古典概型概率计算公式,可得答案.
解答 解:(Ⅰ)3个黑子记为A1,A2,A3,2个白子记为B1,B2.
从袋中随机取出两个棋子,所有可能的结果有:
{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},
{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种.…(2 分)
用M表示“取出的两个棋子颜色相同”,其所有可能的结果有:
{A1,A2},{A1,A3},{A2,A3},{B1,B2},共4种.…(4 分)
∴$P(M)=\frac{4}{10}=\frac{2}{5}$.…(6 分)
(Ⅱ)从袋中随机取出一个棋子,将棋子放回后再从袋中随机取出一个棋子,
其所有可能的结果有:
(A1,A1),(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A2,A1),(A2,A2),(A2,A3),(A2,B1),(A2,B2),
(A3,A1),(A3,A2),(A3,A3),(A3,B1),(A3,B2),
(B1,A1),(B1,A2),(B1,A3),(B1,B1),(B1,B2),
(B2,A1),(B2,A2),(B2,A3),(B2,B1),(B2,B2),共25种.…(9 分)
用N表示“两次取出的棋子中至少有一个白子”,其所有可能的结果有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),
(A3,B2)(B1,A1),(B1,A2),(B1,A3),(B1,B1),
(B1,B2),(B2,A1),(B2,A2),(B2,A3),(B2,B1),(B2,B2),共16种.…(11分)
∴$P(N)=\frac{16}{25}$.…(13分)
点评 本题考查的知识点是古典概型概率计算公式,难度不大,属于基础题.

 某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185) | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
 2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | 0~50 | 51~200 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
(1)求直方图中x的值;
(2)计算一年中空气质量为良和轻微污染的总天数;
(3)求该城市一年中每天空气质量不为良且不为轻微污染的概率.
| A. | -1 | B. | 3 | C. | 11 | D. | 12 |
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
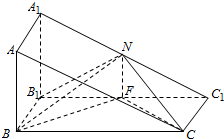 直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.
直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.