题目内容

13．已知命题p：函数y=f（x）在区间[a，b]上单调递增，命题q：函数y=f（x）单调递增区间为[a，b]，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义进行判断即可．

解答 解：若函数y=f（x）单调递增区间为[a，b]，则函数y=f（x）在区间[a，b]上单调递增，即必要性成立，
若f（x）=x在[1，2]上递增，但函数f（x）=x的递增区间为（-∞，+∞），故充分性不成立，
故p是q的必要不充分条件，
故选：B．

点评 本题主要考查充分条件和必要条件的判断，比较基础．

练习册系列答案
相关题目
3．在△ABC中，角A，B，C的所对的边分别为a，b，c，且a2+b2=ab+c2．
（Ⅰ） 求tan（C-$\frac{π}{4}$）的值；
（Ⅱ） 若c=$\sqrt{3}$，求S△ABC的最大值．
4．某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如图所示．
（1）请先求出频率分布表中①、②位置相应数据，再在答题纸上完成下列频率分布直方图；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官进行面试，求：第4组至少有一名学生被考官A面试的概率？
组号分组频数频率
第1组[160，165）50.050
第2组[165，170）①0.350
第3组[170，175）30②
第4组[175，180）200.200
第5组[180，185）100.100
合计1001.00
1．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥1}\\{y-2≤0}\end{array}\right.$，则目标函数z=3x+y的最大值为（　　）
A．-1B．3C．11D．12
8．为得到函数y=sin（x+$\frac{π}{6}$）的图象，可将函数y=sinx的图象向左平移m个单位长度，或向右平移n个单位长度（m，n均为正数，则|m-n|的最小值是（　　）
A．$\frac{π}{3}$B．$\frac{2π}{3}$C．πD．2π
18．5位男生与5位女生排成一排，男生甲与男生乙之间有且只有2位女生，女生不排在两端，这样的排列种数为（　　）
A．5760B．57600C．2880D．28800
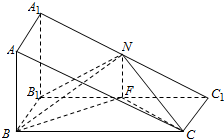5．直三棱柱ABC-A1B1C1中，AB=BB1=$\frac{1}{2}$BC，∠ABC=90°，N、F分别是A1C1、B1C1的中点．
（Ⅰ）求证：CF⊥平面NFB；
（Ⅱ）求二面角C-BN-B1的余弦值．
2．光点随机出现在圆C1：4x2+4y2=π2的内部，则光点出现曲线C2：y2-cos2x=0，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]内部的概率为$\frac{16}{{π}^{3}}$．
17．若对于定义在R上的函数f（x），其图象是连续的，且存在常数λ（λ∈R），使得f（x+λ）+λf（x）=0对任意的实数x成立，则称f（x）是λ一伴随函数，下列对于λ一伴随函数的叙述不正确的是①②
①f（x）=0是唯一的一个常值λ一伴随函数；
②f（x）=x2是一个λ一伴随函数；
③f（x）=2x是一个λ一伴随函数；
④$\frac{1}{2}$一伴随函数至少有一个零点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网