题目内容
已知正四棱柱 中,
中, =
= ,
, 为
为 重点,则异面直线
重点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
 中,
中, =
= ,
, 为
为 重点,则异面直线
重点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )A. | B. | C. | D. |
B
 |
连
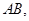 则
则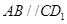 ;所以
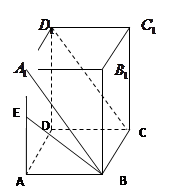
;所以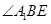 就是异面直线BE与CD1所形成的角;设
就是异面直线BE与CD1所形成的角;设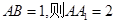

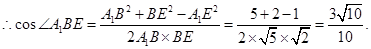
故选B

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
题目内容
 中,
中, =
= ,
, 为
为 重点,则异面直线
重点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )A. | B. | C. | D. |
 |
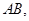 则
则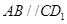 ;所以
;所以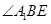 就是异面直线BE与CD1所形成的角;设
就是异面直线BE与CD1所形成的角;设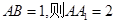

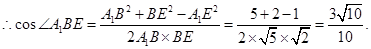

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案