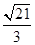题目内容
（本小题满分13分）如图，E为矩形ABCD所在
平面外一点，
平面ABE，AE=EB=BC=2，F为
CE是的点，且
平面ACE，
（1）求证：
平面BCE；
（2）求三棱锥C—BGF的体积。
平面外一点，
平面ABE，AE=EB=BC=2，F为CE是的点，且
平面ACE，（1）求证：
平面BCE；（2）求三棱锥C—BGF的体积。
解：（1）证明：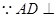
平面ABE，AD//BC。
平面ABE，则
…………3分
又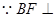
平面ACE，则
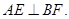…………5分
平面BCE。…………7分
（2）由题意，得G是AC的中点，连FG，
而BC=BE，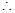
F是EC的中点…………9分
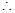AE//FG，且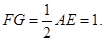
而平面BCE,∴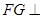
平面BＣＦ。…………11分
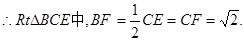
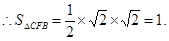
…………13分
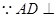平面ABE，AD//BC。 平面ABE，则…………3分又
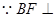平面ACE，则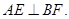…………5分平面BCE。…………7分（2）由题意，得G是AC的中点，连FG，
而BC=BE，
F是EC的中点…………9分AE//FG，且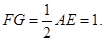而
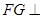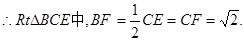
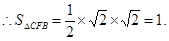
平面BCE,∴平面BＣＦ。…………11分…………13分略
练习册系列答案
阅读快车系列答案
相关题目
中，
、
分别为
、
的中点。
求二面角
的大小。
中，
=
，
为
与
所成角的余弦值为( )
倍，P为侧棱SD上的点。
内的任何直线都平行平面
，则
平面
，平面
平面
，那么直线
平面
，直线
，则
内的一条直线平行，则m//
，则过
，则
