题目内容
已知函数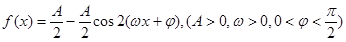 的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且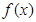 的最大值为2.
的最大值为2.
(Ⅰ)求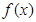 的单调递增区间;
的单调递增区间;
(Ⅱ)计算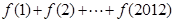 ;
;
(Ⅲ)设函数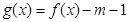 ,试讨论函数
,试讨论函数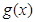 在区间[1,4]上的零点情况.
在区间[1,4]上的零点情况.
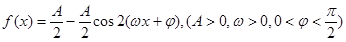 的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且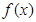 的最大值为2.
的最大值为2.(Ⅰ)求
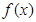 的单调递增区间;
的单调递增区间;(Ⅱ)计算
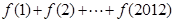 ;
;(Ⅲ)设函数
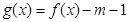 ,试讨论函数
,试讨论函数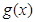 在区间[1,4]上的零点情况.
在区间[1,4]上的零点情况.(Ⅰ)
(Ⅱ)
(Ⅲ) 见解析(Ⅲ)
见解析(Ⅲ)

(Ⅱ)

(Ⅲ)
 见解析(Ⅲ)
见解析(Ⅲ)(I)根据题目给的条件可A=2,T=4,可得 ,再根据图像过点(1,2),
,再根据图像过点(1,2),
可求出 .从而确定f(x)的表达式进而可求出其单调增区间.
.从而确定f(x)的表达式进而可求出其单调增区间.
 ,
,
由于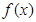 的最大值为2且A>0,
的最大值为2且A>0,
∴ 所以 即A=2
即A=2
∴ ,又函数
,又函数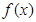 的图象过点(1,2)则
的图象过点(1,2)则

∴
由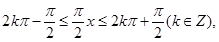 得
得

∴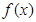 的单调增区间是
的单调增区间是
(II)由于周期为4,所以只需要求出f(1),f(2),f(3),f(4)的值,然后即可知 .
.
由(Ⅰ)知 ,
,
∴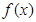 的周期为4,而2012=4×503
的周期为4,而2012=4×503
且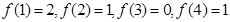
∴原式
(III)解本小题的关键是知道
函数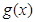 的零点个数即为函数
的零点个数即为函数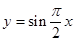 的图象与直线
的图象与直线 的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
函数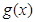 的零点个数即为函数
的零点个数即为函数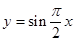 的图象与直线
的图象与直线 的交点个数.
的交点个数.
在同一直角坐标系内作出这两个函数的图象(如下图所示),

由图象可知:
1)当 或
或 时,函数
时,函数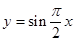 的图象与直线
的图象与直线 无公共点,即函数
无公共点,即函数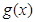 无零点;
无零点;
2)当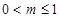 或
或 时,函数
时,函数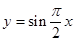 的图象与
的图象与
直线 有一个公共点,即函数
有一个公共点,即函数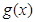 有一个零点;
有一个零点;
3)当 时,函数
时,函数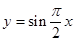 的图象与
的图象与
直线 有两个公共点,即函数
有两个公共点,即函数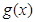 有两个零点.
有两个零点.
 ,再根据图像过点(1,2),
,再根据图像过点(1,2),可求出
 .从而确定f(x)的表达式进而可求出其单调增区间.
.从而确定f(x)的表达式进而可求出其单调增区间. ,
,由于
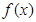 的最大值为2且A>0,
的最大值为2且A>0,∴ 所以
 即A=2
即A=2∴
 ,又函数
,又函数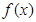 的图象过点(1,2)则
的图象过点(1,2)则
∴

由
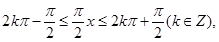 得
得
∴
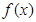 的单调增区间是
的单调增区间是
(II)由于周期为4,所以只需要求出f(1),f(2),f(3),f(4)的值,然后即可知
 .
.由(Ⅰ)知
 ,
,∴
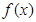 的周期为4,而2012=4×503
的周期为4,而2012=4×503且
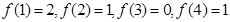
∴原式

(III)解本小题的关键是知道

函数
 的零点个数即为函数
的零点个数即为函数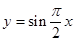 的图象与直线
的图象与直线 的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
函数
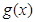 的零点个数即为函数
的零点个数即为函数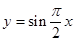 的图象与直线
的图象与直线 的交点个数.
的交点个数.在同一直角坐标系内作出这两个函数的图象(如下图所示),

由图象可知:
1)当
 或
或 时,函数
时,函数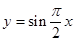 的图象与直线
的图象与直线 无公共点,即函数
无公共点,即函数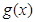 无零点;
无零点;2)当
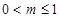 或
或 时,函数
时,函数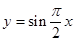 的图象与
的图象与直线
 有一个公共点,即函数
有一个公共点,即函数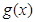 有一个零点;
有一个零点;3)当
 时,函数
时,函数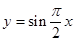 的图象与
的图象与直线
 有两个公共点,即函数
有两个公共点,即函数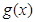 有两个零点.
有两个零点.
练习册系列答案
相关题目
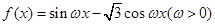 的图象与x轴的两个相邻交点的距离
的图象与x轴的两个相邻交点的距离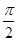 ,若将函数
,若将函数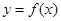 的图象向左平移
的图象向左平移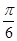 个单位长度得到函数
个单位长度得到函数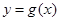 的图象,则
的图象,则
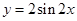


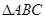 中,若
中,若 ,
, ,则角C的大小为( )
,则角C的大小为( )

 或
或
 .
. 的单调递增区间;
的单调递增区间; 的集合.
的集合. 为单位圆在第一象限内圆弧上的动点,
为单位圆在第一象限内圆弧上的动点, ,设
,设 ,过
,过 ,并交直线
,并交直线 于点
于点 .
.
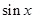 表示) ;
表示) ; 能否为
能否为 ?若能,求出点
?若能,求出点 的面积的最大值,并求出相应
的面积的最大值,并求出相应 值.
值. 的图像 ( )
的图像 ( )  成中心对称
成中心对称 成轴对称
成轴对称 的图像,只需将
的图像,只需将 的图像
的图像  个单位
个单位 个单位
个单位 个单位
个单位 .
. 的最小正周期;
的最小正周期;  时,求函数
时,求函数 的值;
的值;
 的最小正周期为
的最小正周期为 ,则
,则 的值为( )
的值为( )