题目内容
、在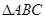 中,若
中,若 ,
, ,则角C的大小为( )
,则角C的大小为( )
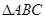 中,若
中,若 ,
, ,则角C的大小为( )
,则角C的大小为( )A. | B. | C. 或 或 | D. 或 或 |
A
解:由3sinA+4cosB=6①,3cosA+4sinB=1②,
①2+②2得:(3sinA+4cosB)2+(3cosA+4sinB)2=37,
化简得:9+16+24(sinAcosB+cosAsinB)=37,
即sin(A+B)=sin(π-C)="sinC=1" 2 ,又C∈(0,π),
2 ,又C∈(0,π),
所以∠C的大小为π 6 或5
6 或5 6 π,
6 π,
若C="5" 6 π,得到A+B=π
6 π,得到A+B=π  6 ,则cosA>
6 ,则cosA>
 2 ,所以3cosA>
2 ,所以3cosA> >1,
>1,
则3cosA+4sinB>1与3cosA+4sinB=1矛盾,所以C≠5 6 π,
6 π,
所以满足题意的C的值为π 6 .
6 .
故选A
①2+②2得:(3sinA+4cosB)2+(3cosA+4sinB)2=37,
化简得:9+16+24(sinAcosB+cosAsinB)=37,
即sin(A+B)=sin(π-C)="sinC=1"
 2 ,又C∈(0,π),
2 ,又C∈(0,π),所以∠C的大小为π
 6 或5
6 或5 6 π,
6 π,若C="5"
 6 π,得到A+B=π
6 π,得到A+B=π  6 ,则cosA>
6 ,则cosA>
 2 ,所以3cosA>
2 ,所以3cosA> >1,
>1,则3cosA+4sinB>1与3cosA+4sinB=1矛盾,所以C≠5
 6 π,
6 π,所以满足题意的C的值为π
 6 .
6 .故选A

练习册系列答案
相关题目

 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴; 的图象经怎样的变换得到.
的图象经怎样的变换得到.
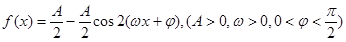 的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且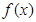 的最大值为2.
的最大值为2.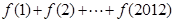 ;
;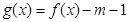 ,试讨论函数
,试讨论函数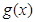 在区间[1,4]上的零点情况.
在区间[1,4]上的零点情况.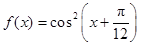 ,
,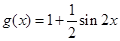 .
.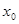 是函数
是函数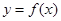 的一个零点,求
的一个零点,求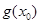 的值;
的值;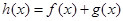 的单调递增区间.
的单调递增区间. 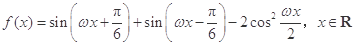 (其中
(其中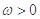 ).
).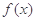 的值域;
的值域; 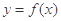 的图象与直线
的图象与直线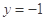 的两个相邻交点间的距离为
的两个相邻交点间的距离为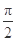 ,求函数
,求函数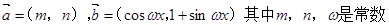 且
且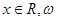 >0,设函数
>0,设函数 的周期为
的周期为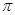 ,且当
,且当 时,函数取最大值2.
时,函数取最大值2. 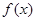 的解析式,并写出
的解析式,并写出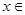
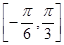 时,求
时,求 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( ) 向右平移
向右平移 个单位
个单位  向左平移
向左平移 向右平移
向右平移 个单位
个单位  向左平移
向左平移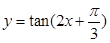 的图像向右
的图像向右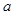 平移个单位后所得的图像关于点
平移个单位后所得的图像关于点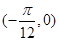 中心对称.则
中心对称.则



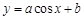 (
(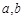 为常数)的最大值为1,最小值为
为常数)的最大值为1,最小值为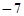 ,则
,则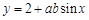 的最大值_______.
的最大值_______.