题目内容
14.f(x)=sinx+tanx+2,x∈[-$\frac{π}{4}$,$\frac{π}{4}$],f(x)最大值为M,最小值为m,M+m为( )| A. | 4 | B. | -4 | C. | 2 | D. | 0 |
分析 令g(x)=sinx+tanx,可判断函数g(x)为定义域内的奇函数,设出其在定义域内的最大值和最小值,则函数f(x)的最大值和最小值可求,答案可求.
解答 解:令g(x)=sinx+tanx,
∵x∈[-$\frac{π}{4}$,$\frac{π}{4}$],且g(-x)=sin(-x)+tan(-x)=-sinx-tanx=-(sinx+tanx)=-g(x).
∴g(x)定义域内的奇函数,
设g(x)在x∈[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值为N,则最小值为-N,
∴M=N+2,m=-N+2,
∴M+m=N+2+(-N+2)=4.
故选:A.
点评 本题考查三角函数的最值,着重考查了函数奇偶性的性质,考查数学转化思想方法,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
2.已知角α的终边上一点P(-3,4),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
6.如图,若f(x)=log3x,g(x)=log2x,输入x=0.25,则输出h(x)=( )

| A. | 0.25 | B. | $\frac{1}{2}$log322 | C. | -21log32 | D. | -2 |
3.已知二次函数y=6x-2x2-m的值恒小于零,那么实数m的取值范围为( )
| A. | m=$\frac{9}{2}$ | B. | m>$\frac{9}{2}$ | C. | m=9 | D. | m<9 |
4.复数z=(1-i)•i的共轭复数$\overline{z}$等于( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |

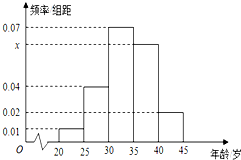 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].