题目内容
9．已知函数g（x）=x-$\sqrt{3x+1}，h（x）=\frac{1}{2x}+\sqrt{3x+1}$，那么函数f（x）=g（x）+h（x）的解析式是f（x）=x+$\frac{1}{2x}$，（x≥-$\frac{1}{3}$，且x≠0）．分析 根据已知，求出函数g（x），h（x）的定义域，进而可得函数f（x）=g（x）+h（x）的解析式．
解答 解：∵函数g（x）=x-$\sqrt{3x+1}$，（x≥-$\frac{1}{3}$），
h（x）=$\frac{1}{2x}+\sqrt{3x+1}$，（x≥-$\frac{1}{3}$，且x≠0）
∴函数f（x）=g（x）+h（x）=x+$\frac{1}{2x}$，（x≥-$\frac{1}{3}$，且x≠0）
故答案为：x+$\frac{1}{2x}$，（x≥-$\frac{1}{3}$，且x≠0）
点评 本题考查的知识点是函数的解析式及求法，函数的定义域，解答时一定要注意两个基本函数定义域对复合函数定义域的影响．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
19．为了检测某种产品的直径（单位mm），抽取了一个容量为100的样本，其频率分布表（不完整）如下：
（Ⅰ）完成频率分布表；
（Ⅱ）画出频率分布直方图；
（Ⅲ）据上述图表，估计产品直径落在[10.95，11.35）范围内的可能性是百分之几？
（Ⅳ）从[11.35，11.45）∪[11.55，11.65）中抽取两个产品，直径分别记作为x，y，求|x-y|＜0.1的概率
| 分组 | 频数累计 | 频数 | 频率 |
| [10.75，10.85） | 6 | 6 | 0.06 |
| [10.85，10.95） | 15 | 9 | 0.09 |
| [10.95，11.05） | 30 | 15 | 0.15 |
| [11.05，11.15） | 48 | 18 | 0.18 |
| [11.15，11.25） | |||
| [11.25，11.35） | 84 | 12 | 0.12 |
| [11.35，11.45） | 92 | 8 | 0.08 |
| [11.45，11.55） | 98 | 6 | 0.06 |
| [11.55，11.65） | 100 | 2 | 0.02 |
（Ⅱ）画出频率分布直方图；
（Ⅲ）据上述图表，估计产品直径落在[10.95，11.35）范围内的可能性是百分之几？
（Ⅳ）从[11.35，11.45）∪[11.55，11.65）中抽取两个产品，直径分别记作为x，y，求|x-y|＜0.1的概率
20．过点（3，-2）且与椭圆4x2+9y2=36有相同焦点的椭圆的方程是（ ）
| A． | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | B． | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | C． | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
17．若非零实数a，b满足a＞b，则（ ）
| A． | $\frac{1}{a}＜\frac{1}{b}$ | B． | $\frac{1}{a^2}＞\frac{1}{b^2}$ | C． | a2＞b2 | D． | 2a＞2b |
如图是某单位200名职工的年龄分布情况，现要从中抽取40名职工样本，用系统抽样法，将全体职工随机按1～200编号，并按
1．直线y=a与y=tanx的图象的相邻两个交点的距离是（ ）
| A． | $\frac{π}{2}$ | B． | π | ||
| C． | 2π | D． | 与a的值的大小有关 |
19．
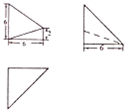已知某空间几何体的三视图如图所示，则该几何体的体积是（ ）
已知某空间几何体的三视图如图所示，则该几何体的体积是（ ）| A． | 16 | B． | 32 | C． | 36 | D． | 48 |