题目内容
4.复数z=(1-i)•i的共轭复数$\overline{z}$等于( )| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
分析 直接由复数代数形式的乘法运算化简复数z,则z的共轭复数可求.
解答 解:∵z=(1-i)•i=1+i,
∴$\overline{z}$=1-i.
故选:B.
点评 本题考查了复数代数形式的乘法运算,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.若直线过点M(1,2),N(4,2+$\sqrt{3}$),则此直线的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.已知函数f(x)=xex,对?x∈R,a-f(x)≤0恒成立,则a的最大值为( )
| A. | -e | B. | e | C. | -e-1 | D. | e-1 |
19.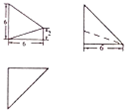 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )
 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )| A. | 16 | B. | 32 | C. | 36 | D. | 48 |
9.某次运动会在我市举行,为了搞好接待工作,组委会招募了18名男志愿者和12名女志愿者,调查发现,男、女志愿者中分别由11人和5人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)从女志愿者中抽取2人参加接待工作,若其中喜爱运动的人数为ξ,求ξ的分布列和数学期望Eξ.
参考公式:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
(1)根据以上数据完成以下2×2列联表:
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 18 | |
| 女 | 5 | 12 | |
| 总计 | 30 |
(3)从女志愿者中抽取2人参加接待工作,若其中喜爱运动的人数为ξ,求ξ的分布列和数学期望Eξ.
参考公式:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(x2≥x0) | 0.40 | 0.25 | 0.10 | 0.010 |
| x0 | 0.708 | 1.323 | 2.706 | 6.635 |
16.抛物线y2=2px(p>0)的焦点为F,点A,B在此抛物线上,且∠AFB=90°,弦AB的中点M在该抛物线准线上的射影为M′,则$\frac{|MM′|}{|AB|}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}(4-a)x,x<2\\{a^x},x≥2\end{array}\right.$在R上单调递增,则a的取值范围是( )
| A. | (1,4] | B. | (2,4) | C. | [2,4) | D. | (4,+∞) |
17.在等比数列{an}前n项和Sn=5n-1,则a12+a22+a32+…+an2等于( )
| A. | (5n-1)2 | B. | 52n-1 | C. | $\frac{2}{3}$(52n+1+1) | D. | $\frac{2}{3}$(52n-1) |