题目内容
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在△BCD内运动(含边界),设 =α
=α +β
+β ,则α+β的最大值是( )
,则α+β的最大值是( )

 =α
=α +β
+β ,则α+β的最大值是( )
,则α+β的最大值是( )
A. | B. | C. | D. |
B
【思路点拨】建立坐标系,设P(x,y),求出α+β与x,y的关系,运用线性规划求解.
解:以A为原点,AB所在直线为x轴建立平面直角坐标系,则D(0,1),B(3,0),C(1,1),设P(x,y).
∴ =(x,y),
=(x,y), =(0,1),
=(0,1), =(3,0).
=(3,0).
∵ =α
=α +β
+β ,
,
即(x,y)=α(0,1)+β(3,0)=(3β,α),
∴ ∴
∴ ∴α+β=
∴α+β= +y.
+y.
由线性规划知识知在点C(1,1)处 +y取得最大值
+y取得最大值 .
.
解:以A为原点,AB所在直线为x轴建立平面直角坐标系,则D(0,1),B(3,0),C(1,1),设P(x,y).
∴
 =(x,y),
=(x,y), =(0,1),
=(0,1), =(3,0).
=(3,0).∵
 =α
=α +β
+β ,
,即(x,y)=α(0,1)+β(3,0)=(3β,α),
∴
 ∴
∴ ∴α+β=
∴α+β= +y.
+y.由线性规划知识知在点C(1,1)处
 +y取得最大值
+y取得最大值 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
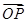 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).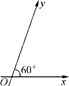
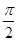
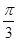
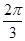
 ,则α与β的夹角θ的取值范围是 .
,则α与β的夹角θ的取值范围是 . ;③若△ABC中,a="5,b=8," c=7,则
;③若△ABC中,a="5,b=8," c=7,则 ·
· =20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .
=20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .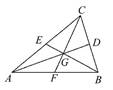
 =
=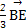
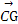 =2
=2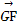
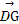 =
=
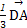 +
+ =
=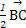
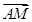 ·
·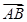 +
+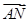 ·
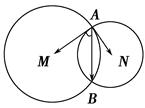
·
 中,
中,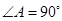 ,
,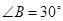 ,
,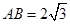 ,
,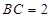 ,点
,点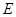 在线段
在线段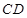 上,若
上,若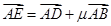 ,则
,则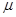 的取值范围是( )
的取值范围是( )


 =m,
=m, =n,则
=n,则 = .
= .