题目内容
17.已知在三棱锥P-ABC中,PA=4,AC=2$\sqrt{7}$,PB=BC=2$\sqrt{3}$,PA⊥平面PBC,则三棱锥P-ABC的内切球的表面积为( )| A. | $\frac{3}{2}$π | B. | 3π | C. | $\frac{9}{4}$π | D. | 4π |
分析 确定△PBC为等边三角形,△ABC为等腰三角形,分别求出四面体P-ABC的内切球半径,即可得出结论.
解答 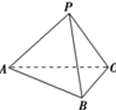 解:由题意,已知PA⊥面PBC,PA=4,PB=BC=2$\sqrt{3}$,AC=2$\sqrt{7}$,
解:由题意,已知PA⊥面PBC,PA=4,PB=BC=2$\sqrt{3}$,AC=2$\sqrt{7}$,
所以,由勾股定理得到:AB=2$\sqrt{7}$,PC=2$\sqrt{3}$,
所以,△PBC为等边三角形,△ABC为等腰三角形
等边三角形PBC所在的小圆的直径PD=$\frac{2\sqrt{3}}{sin60°}$=4,
那么,四面体P-ABC的外接球直径2R=4$\sqrt{2}$,所以,R=2$\sqrt{2}$,
VP-ABC=$\frac{1}{3}$S△PBC×PA=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×12×4=4$\sqrt{3}$,
表面积S=$\frac{1}{2}×$2$\sqrt{3}×$4×2+$\frac{\sqrt{3}}{4}$×12+$\frac{1}{2}×$2$\sqrt{3}×$5=16$\sqrt{3}$,
设内切球半径为r,那么4$\sqrt{3}$=$\frac{1}{3}×$16$\sqrt{3}$r,所以r=$\frac{3}{4}$,
所以三棱锥P-ABC的内切球的表面积为4π×$\frac{9}{16}$=$\frac{9π}{4}$,
故选:C.
点评 本题考查四面体P-ABC的内切球表面积,考查学生分析解决问题的能力,确定三棱锥P-ABC的内切球的半径是关键,属于中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
11.若tanα=2,则$\frac{sinα-cosα}{2sinα+cosα}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | 3 | D. | -2 |
2.某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(注:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,a=$\overline{y}-b\overline{x}$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(注:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,a=$\overline{y}-b\overline{x}$.
9.复数z满足(-1+i)z=(1+i)2,其中i为虚数单位,则|z|=( )
| A. | 2 | B. | -2 | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
6.已知x,y∈(-∞,0),且x+y=-1,则xy+$\frac{1}{xy}$有( )
| A. | 最大值$\frac{17}{4}$ | B. | 最小值$\frac{17}{4}$ | C. | 最小值-$\frac{17}{4}$ | D. | 最大值-$\frac{17}{4}$ |
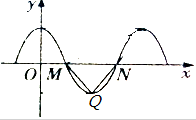 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.