题目内容
8.将函数f(x)=2sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,则b的最小值为$\frac{59π}{12}$.分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得g(x)的解析式,再由y=g(x)在[0,b](b>0)上至少含有10个零点,可得方程sin2x=-$\frac{1}{2}$至少有10个解,则b的最小值4×π+$\frac{11π}{12}$,计算可得结果.
解答 解:将函数f(x)=2sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,可得y=2sin[2(x+$\frac{π}{6}$)-$\frac{π}{3}$]=2sin2x的图象;
再向上平移1个单位,得到函数y=g(x)=2sin2x+1的图象,
再由y=g(x)在[0,b](b>0)上至少含有10个零点,可得方程sin2x=-$\frac{1}{2}$至少有10个解,
则b的最小值4×π+$\frac{11π}{12}$=$\frac{59π}{12}$,
故答案为:$\frac{59π}{12}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的特征,属于基础题.

练习册系列答案
相关题目
3.已知a=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,b=log5$\frac{1}{3}$,c=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
17.已知在三棱锥P-ABC中,PA=4,AC=2$\sqrt{7}$,PB=BC=2$\sqrt{3}$,PA⊥平面PBC,则三棱锥P-ABC的内切球的表面积为( )
| A. | $\frac{3}{2}$π | B. | 3π | C. | $\frac{9}{4}$π | D. | 4π |
18.设双曲线方程mx2-ny2=1(mn≠0),则“离心率e=$\sqrt{2}$”是“m=n”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
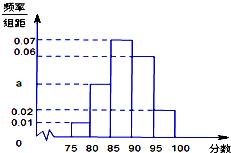 某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直
某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直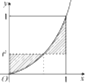 如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.
如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.