题目内容
5.已知角α=1200°(1)将α改写成β+2kπ(k∈Z,0≤β≤2π)的形式,并指出α是第几象限的角;
(2)在区间[-4π,π]上找出与α终边相同的角.
分析 (1)利用终边相同的假的表示方法,把角α写成β+2kπ(k∈Z,0≤β≤2π)的形式,然后指出它是第几象限的角;
(2)利用终边相同的角的表示方法,通过k的取值,求出α,即可.
解答 解:(1)∵α=1200°=$1200×\frac{π}{180}rad$=$\frac{20π}{3}=3×2π+\frac{2π}{3}rad$,
又∵$\frac{π}{2}<\frac{2π}{3}<π$,
∴角α与$\frac{2π}{3}$的终边相同,角α是第二象限的角.
(2)∵与角α终边相同的角(含角α在内)为$2kπ+\frac{2π}{3}k∈Z$,
∴由$-4π≤2kπ+\frac{2π}{3}≤πk∈Z$得:k=-2,k=-1时,不等式成立.
∴在区间[-4π,π]上与角α终边相同的角是$-\frac{10π}{3},-\frac{4π}{3}$.…(12分)
点评 本题考查终边相同角的表示方法,基本知识的考查.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:

(Ⅰ)写出频率分布直方图中的a的值,并作出甲种酸奶日销售量的频率分布直方图;
答:a=0.015;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s12,s22,试比较s12与s22的大小.(只需写出结论).
答:s12<s22.

| 分组 (日销售量) | 频率 (甲种酸奶) |
| [0,10] | 0.10 |
| (10,20] | 0.20 |
| (20,30] | 0.30 |
| (30,40] | 0.25 |
| (40,50] | 0.15 |
答:a=0.015;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s12,s22,试比较s12与s22的大小.(只需写出结论).
答:s12<s22.
17.已知在三棱锥P-ABC中,PA=4,AC=2$\sqrt{7}$,PB=BC=2$\sqrt{3}$,PA⊥平面PBC,则三棱锥P-ABC的内切球的表面积为( )
| A. | $\frac{3}{2}$π | B. | 3π | C. | $\frac{9}{4}$π | D. | 4π |
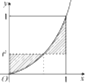 如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.
如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.