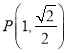题目内容
【题目】设数列{an}的前n项和为Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{bn}满足an﹣an﹣1=bna ![]() ,求数列{bn}的n前项和Tn;
,求数列{bn}的n前项和Tn;
(3)是否存在实数λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() ,n∈N*.
,n∈N*.
∴ ![]() ①
①
∴当n≥2时, ![]() ②
②
由①﹣②,得
2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).
∵2an=2Sn﹣2Sn﹣1
∴2an=nan+1﹣(n﹣1)an﹣n(n+1),
∴ ![]() ,
,
∴数列 ![]() 是以首项为
是以首项为 ![]() ,公差为1的等差数列.
,公差为1的等差数列.
∴ ![]() ,
,
∴ ![]() ,当n=1时,上式显然成立.
,当n=1时,上式显然成立.
∴ ![]()
(2)an﹣an﹣1=bna ![]() bn=
bn= ![]() =
= ![]() =
= ![]() .
.
∴Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .①
.①
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .②
.②
由①﹣②,得
![]() Tn=
Tn= ![]() +2(
+2( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]() .
.
= ![]() +2
+2 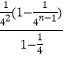 ﹣
﹣ ![]() .
.
∴Tn= ![]() ﹣
﹣ ![]() ,n∈N+
,n∈N+
(3)λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0λ(2n﹣
≥0λ(2n﹣ ![]() )+2n+
)+2n+ ![]() ≥0,(n=2,4,6,8,10…)λ(2n﹣
≥0,(n=2,4,6,8,10…)λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,
)2+2≥0,
令t=2n﹣ ![]() ,则t≥
,则t≥ ![]() ,
,
原不等式λt+t2+2≤0≥﹣(t+ ![]() ).
).
∵t+ ![]() 在(
在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴t+ ![]() ≥
≥ ![]() +
+ ![]() .
.
∴λ≥﹣ ![]()
【解析】(1)需要分类讨论:n=1和n≥2两种情况下的通项公式.当n≥2时,根据已知条件可以推知2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).2an=nan+1﹣(n﹣1)an﹣n(n+1),由着两个式子可以得到数列 ![]() 是以首项为
是以首项为 ![]() ,公差为1的等差数列.由此写出通项公式即可;(2)由an﹣an﹣1=bna
,公差为1的等差数列.由此写出通项公式即可;(2)由an﹣an﹣1=bna ![]() 可得bn=
可得bn= ![]() =
= ![]() =
= ![]() .再利用“错位相减法”与等比数列的求和公式即可得出;(3)将已知不等式变形为λ(2n﹣
.再利用“错位相减法”与等比数列的求和公式即可得出;(3)将已知不等式变形为λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,然后结合函数的单调性来求λ的取值范围.
)2+2≥0,然后结合函数的单调性来求λ的取值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标 |
|
|
|
|
|
|
钻探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
(1)在散点图中![]() 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即: ![]() )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: 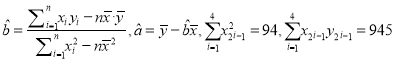 )
)
(3)设出油量与钻探深度的比值![]() 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号![]() 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率.