题目内容
【题目】已知抛物线C：y2=2px过点P（1，1）.过点（0，
）作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP、ON交于点A，B，其中O为原点.
（Ⅰ）求抛物线C的方程，并求其焦点坐标和准线方程；
（Ⅱ）求证：A为线段BM的中点.
【答案】（Ⅰ）抛物线C的焦点坐标为（
，0），准线方程为
.
（Ⅱ）详见解析
【解析】解：（Ⅰ）由抛物线C：
过点P（1，1），得
.
所以抛物线C的方程为
.
抛物线C的焦点坐标为（，0），准线方程为.
（Ⅱ）由题意，设直线l的方程为
（
），l与抛物线C的交点为
，
.
由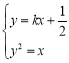
，得
.
则
，
.
因为点P的坐标为（1，1），所以直线OP的方程为
，点A的坐标为
.
直线ON的方程为
，点B的坐标为
.
因为
，
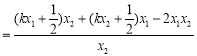
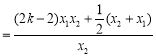
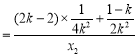
所以
.
故A为线段BM的中点.
练习册系列答案
相关题目
【题目】某学校高一 、高二 、高三三个年级共有 
名教师，为调查他们的备课时间情况，通过分层
抽样获得了
名教师一周的备课时间 ，数据如下表（单位 ：小时）：
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
（1）试估计该校高三年级的教师人数 ；
（2）从高一年级和高二年级抽出的教师中，各随机选取一人，高一年级选出的人记为甲 ，高二年级选出的人记为乙 ，求该周甲的备课时间不比乙的备课时间长的概率 ；
（3）再从高一、高二、高三三个年级中各随机抽取一名教师，他们该周的备课时间分别是
（单位： 小时），这三个数据与表格中的数据构成的新样本的平均数记为
，表格中的数据平均数记为
，试判断
与
的大小. （结论不要求证明）
