题目内容

4．设圆的半径为4，沿x轴正向滚动，开始时圆与x轴相切于原点O．
（1）写出该圆初始位置的极坐标方程；
（2）记圆上动点为M，开始时M位于O处，它随圆的滚动而改变位置，写出圆滚动一周时M点的轨迹方程．

分析 （1）写出该圆初始位置的普通方程，可得极坐标方程；
（2）M点的轨迹是摆线，可得方程．

解答 解：（1）圆的初始位置是以（0，2）为圆心，2为半径的圆，普通方程为x2+（y-2）2=4，
极坐标方程为ρ=4sinθ；
（2）M点的轨迹是摆线，方程为$\left\{\begin{array}{l}{x=4（t-sint）}\\{y=4（1-cost）}\end{array}\right.$，（0≤t≤2π）．

点评 本题考查圆的方程，考查学生分析解决问题的能力，正确转化是关键．

练习册系列答案
相关题目
14．箱子中有4个分别标有号码1、2、3、4的小球，从中随机取出一个记下号码后放回，再随机取出一个记下号码，则两次记下的号码至少一个奇数的概率为$\frac{3}{4}$．
15．在△ABC中，（sinA+sinB）（sinA-sinB）≤sinC（sinC-sinB），则A的取值范围是（　　）
A．（0，$\frac{π}{6}$]B．[$\frac{π}{6}，π$）C．（0，$\frac{π}{3}$]D．[$\frac{π}{3}，π$）
12．已知数列{an}满足a1=1，an=an-1+2n（n≥2，n∈N*），则a4=19．
19．已知复数z=$\frac{a+4i}{1+ai}$，a＞0，且z=$\overline{z}$，若1+ai是关于x的方程x2+bx+c=0的一根，则b，c分别为（　　）
A．4，-8B．2，-5C．-4，8D．-2，5
9．已知函数y=f（x）的图象与y=lnx的图象关于x轴对称，则f（x）=（　　）
A．exB．（$\frac{1}{e}$）xC．-lnxD．|lnx|
16．设函数f（x）=$\frac{{x}^{2}}{1+{x}^{2}}$．
（1）计算f（2）+f（$\frac{1}{2}$）、f（-5）+f（-$\frac{1}{5}$）、f（$\sqrt{2}$）+f（$\frac{\sqrt{2}}{2}$）的值；
（2）根据（1）中的计算结果，归纳猜想关于函数y=f（x）的一般性结论，并给予证明．
13．计算22+42+62+…+1002的算法的程序框图是（　　）
A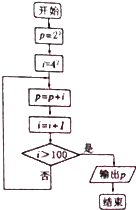．B．C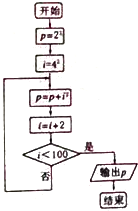．D．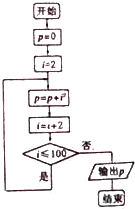
14．（1）解不等式-$\frac{1}{2}{x^2}-x-\frac{3}{2}$＜-2；
（2）已知集合A={x|x2-x-6＜0}，B={x|x2+2x-8＞0}，求A∩B．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网