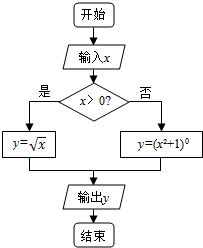
题目内容
9.已知函数y=f(x)的图象与y=lnx的图象关于x轴对称,则f(x)=( )| A. | ex | B. | ($\frac{1}{e}$)x | C. | -lnx | D. | |lnx| |
分析 利用y=f(x)的图象与y=-f(x)的图象关于x轴对称,结合已知,可得答案.
解答 解:∵函数y=f(x)的图象与y=lnx的图象关于x轴对称,
∴f(x)=-lnx,
故选:C.
点评 本题考查的知识点是对数函数的图象和性质,函数图象的对称变换,难度不大,属于基础题.

练习册系列答案
相关题目
19.从某学校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的条形图.
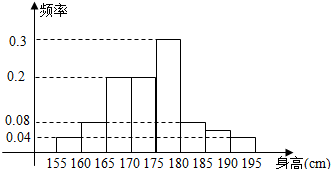
(1)根据已知条件填写下面表格:
(2)估计这所学校高三年级800名学生中身高在175cm以上(含175cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?

(1)根据已知条件填写下面表格:
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 |
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?
17.已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=$\frac{{2}^{-x}-a}{3}$,则f(4)等于( )
| A. | $\frac{16}{3}$ | B. | 5 | C. | -$\frac{16}{3}$ | D. | -5 |
1.若随机变量X~N(1,4),则P(1<X≤3)=( )
(附:若随机变量X~N(μ,σ2)(σ>0),则P(μ-σ<X≤(μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544.
(附:若随机变量X~N(μ,σ2)(σ>0),则P(μ-σ<X≤(μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544.
| A. | 0.6826 | B. | 0.3413 | C. | 0.9544 | D. | 0.4772 |