题目内容
试证明:椭圆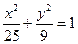 与曲线
与曲线
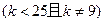 有相同的焦点。
有相同的焦点。
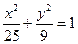 与曲线
与曲线
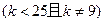 有相同的焦点。
有相同的焦点。证明略
证明:当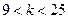 时,
时,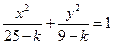 表示焦点在
表示焦点在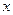 轴上的双曲线,
轴上的双曲线,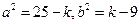 ,∴
,∴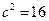 与椭圆
与椭圆 有相同的焦点;当
有相同的焦点;当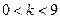 时,
时,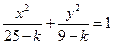 表示焦点在
表示焦点在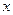 轴上的椭圆,
轴上的椭圆,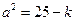 ,
,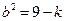 ,∴
,∴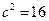 ,此时曲线也与
,此时曲线也与 有相同的焦点,综上,曲线与
有相同的焦点,综上,曲线与 有相同的焦点。
有相同的焦点。
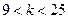 时,
时,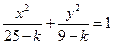 表示焦点在
表示焦点在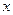 轴上的双曲线,
轴上的双曲线,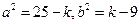 ,∴
,∴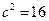 与椭圆
与椭圆 有相同的焦点;当
有相同的焦点;当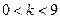 时,
时,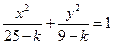 表示焦点在
表示焦点在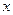 轴上的椭圆,
轴上的椭圆,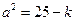 ,
,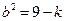 ,∴
,∴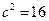 ,此时曲线也与
,此时曲线也与 有相同的焦点,综上,曲线与
有相同的焦点,综上,曲线与 有相同的焦点。
有相同的焦点。
练习册系列答案
相关题目
题目内容
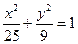 与曲线
与曲线
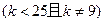 有相同的焦点。
有相同的焦点。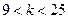 时,
时,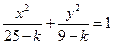 表示焦点在
表示焦点在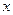 轴上的双曲线,
轴上的双曲线,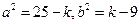 ,∴
,∴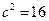 与椭圆
与椭圆 有相同的焦点;当
有相同的焦点;当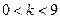 时,
时,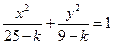 表示焦点在
表示焦点在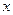 轴上的椭圆,
轴上的椭圆,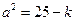 ,
,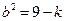 ,∴
,∴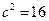 ,此时曲线也与
,此时曲线也与 有相同的焦点,综上,曲线与
有相同的焦点,综上,曲线与 有相同的焦点。
有相同的焦点。