题目内容
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
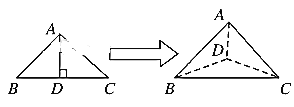
①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
【答案】①②③
【解析】
设等腰直角三角形△ABC的腰为a,则斜边BC=![]() a,
a,
①利用面面垂直的性质定理易证BD⊥平面ADC,又AC平面ADC,从而可知BD⊥AC,可判断①;
②依题意及设法可知,![]()
利用勾股定理可求得![]() ,从而可判断②;
,从而可判断②;
③又因为DA=DB=DC,根据正三棱锥的定义判断;
④作出平面ADC与平面ABC的二面角的平面角,利用BD⊥平面ADC可知,∠BDF为直角,∠BFD不是直角,从而可判断④.
设等腰直角三角形△ABC的腰为a,则斜边BC=![]() a,
a,
D为BC的中点,∴AD⊥BC,
又平面ABD⊥平面ACD,平面ABD∩平面ACD=AD,BD⊥AD,BD平面ABD,
∴BD⊥平面ADC,又AC平面ADC,
∴BD⊥AC,故①正确;
②由A知,BD⊥平面ADC,CD平面ADC,
∴BD⊥CD,又![]() ∴由勾股定理得:
∴由勾股定理得:![]() ,又AB=AC=a,
,又AB=AC=a,
∴△ABC是等边三角形,故②正确;
③∵△ABC是等边三角形,DA=DB=DC,
∴三棱锥D-ABC是正三棱锥,故③正确.
④∵△ADC为等腰直角三角形,取斜边AC的中点F,则DF⊥AC,又△ABC为等边三角形,连接BF,则BF⊥AC,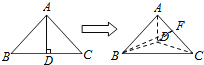
∴∠BFD为平面ADC与平面ABC的二面角的平面角,
由BD⊥平面ADC可知,∠BDF为直角,∠BFD不是直角,故平面ADC与平面ABC不垂直,故④错误;
综上所述,正确的结论是①②③.

练习册系列答案
相关题目