题目内容
12.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中个抽出500 件,量其内径尺寸的结果如下表(表1为甲厂,表2为乙 厂):表1
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
分析 (1)要求两个分厂生产的零件的优质品率,我们可以根据已知中的表格中的数据,及规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品,我们及计算出两个分厂生产的零件的优质品率;
(2)按照分层抽样中,样本中的比例与总体中的比例一致,易得表中各项数据的值,然后我们可以根据列联表中的数据,代入公式K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,计算出k值,然后代入离散系数表,比较即可得到答案.
解答 解:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为$\frac{360}{500}$=72%
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质$\frac{320}{500}$=64%品率估计 …6分
(2)
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | 360 | 320 | 680 |
| 非优质品 | 140 | 180 | 320 |
| 合计 | 500 | 500 | 1000 |
${K}^{2}=\frac{1000×(360×180-320×140)^{2}}{500×500×680×320}≈7.35>6.635$
所以有99%的把握认为“两个分厂生产的零件的质量有差异”. …14分
点评 独立性检验的应用的步骤为:根据已知条件将数据归结到一个表格内,列出列联表,再根据列联表中的数据,代入公式K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,计算出k值,然后代入离散系数表,比较即可得到答案.属于中档题,计算量稍大,但思路明确.

练习册系列答案
相关题目
17.执行如图所示的程序框图,则输出的结果为( )
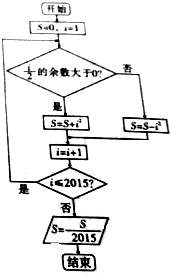

| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |
2.某校通过随机询问100名性别不同的学生是否能做到“光盘”行动,得到所示联表:
附:K2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,则下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
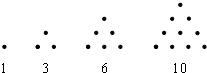 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数: