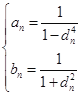Question

【题目】已知点C是平面直角坐标系中的一个动点，过点C且与y轴垂直的直线与直线交于点M，若向量与向量垂直，其中O为坐标原点.

（1）求点C的轨迹方程E；

（2）过曲线E的焦点作互相垂直的两条直线分别交曲线E于A，B，P，Q四点，求四边形APBQ的面积的最小值.

Answer 1

【答案】（1）；（2）32.

【解析】

（1）设点，转化条件得，即可得解；

（2）设直线，直线，，，，，联立方程组可得，，则，求出最小值即可得解.

（1）设点.

由题意，点，则，.

因为向量与向量垂直，

所以.

即.

故点的轨迹方程是.

（2）由（1）知，抛物线E的焦点是，

设直线，则直线.

联立，消去得，

设，，则，.

所以.

设点，，同理可得.

所以

，当且仅当，即时等号成立.

即四边形的面积的最小值为.