题目内容
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为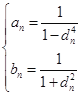 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题(1)直接运用题设中的条件解方程求解;(2)借助题设条件运用充分必要条件进行求解;(3)依据题设条件和三角函数的有关知识进行综合求解
试题解析:(1)∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 为有理数列,∴
为有理数列,∴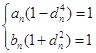 ,∴
,∴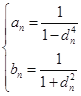 ,以上每一步可逆.
,以上每一步可逆.
(3)![]() ,
,
∴![]() ,∴
,∴![]() 或
或![]()
∵![]() ,∴
,∴![]() ,
,
当![]() 时,∴
时,∴![]()
当![]() 时,∴
时,∴![]()
∴![]() 为有理数列,
为有理数列,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() 为有理数列,
为有理数列,![]() 为无理数列,
为无理数列,
∴![]() ,∴
,∴![]() ,
,
∴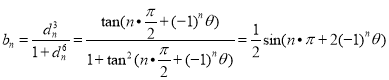
当![]() 时,∴
时,∴![]()
当![]() 时,∴
时,∴![]() ,
,
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目