Question

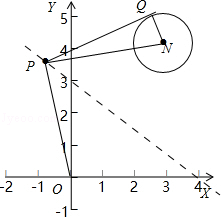
【题目】过动点P作圆：（x﹣3）2+（y﹣4）2=1的切线PQ，其中Q为切点，若|PQ|=|PO|（O为坐标原点），则|PQ|的最小值是 ．

Answer 1

【答案】
【解析】解：根据题意，设P的坐标为（m，n），圆（x﹣3）2+（y﹣4）2=1的圆心为N，则N（3，4） PQ为圆（x﹣3）2+（y﹣4）2=1的切线，则有|PN|2=|PQ|2+|NQ|2=|PQ|2+1，
又由|PQ|=|PO|，
则有|PN|2=|PO|2+1，
即（m﹣3）2+（n﹣4）2=m2+n2+1，
变形可得：6m+8n=24，
即P在直线6x+8y=24上，
则|PQ|的最小值即点O到直线6x+8y=24的距离，
且d= = ；
即|PQ|的最小值是 ；
所以答案是： ．