题目内容
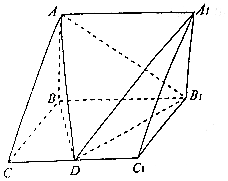
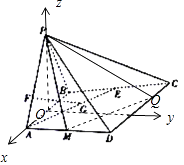
【题目】如图,在四棱锥P﹣ABCD中,侧面PAB⊥底面ABCD,△PAB为正三角形.AB⊥AD,CD⊥AD,点E、M为线段BC、AD的中点,F,G分别为线段PA,AE上一点,且AB=AD=2,PF=2FA. 
(1)确定点G的位置,使得FG∥平面PCD;
(2)试问:直线CD上是否存在一点Q,使得平面PAB与平面PMQ所成锐二面角的大小为30°,若存在,求DQ的长;若不存在,请说明理由.
【答案】
(1)解:在AD上取AN= ![]() AD,过N作NG∥DC,交AE于G,连结FG,FN,
AD,过N作NG∥DC,交AE于G,连结FG,FN,
∵PF=2FA.可得FA= ![]() PA,所以FN∥PD,又NG∥DC,FN∩NG=N,PD∩DC=D,
PA,所以FN∥PD,又NG∥DC,FN∩NG=N,PD∩DC=D,
可得平面FNG∥平面PCD,FG平面FNG,所以FG∥平面PCD
(2)解:作PO⊥AB于O,BA所在直线为x轴,OP所在直线为z轴,在平面ABCD内作AB的垂线为y轴,如图:平面PAB的法向量为: ![]() =(0,1,0),
=(0,1,0),
A(1,0,0),Q(λ,2,0),M(1,1,0),P(0,0, ![]() ),
),
则 ![]() =(﹣1,﹣1,
=(﹣1,﹣1, ![]() ),
), ![]() =(λ﹣1,1,0),
=(λ﹣1,1,0),
设平面PMQ的法向量为: ![]() =(x,y,z),
=(x,y,z),
由 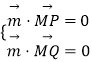 ,可得:
,可得: ![]() ,令x=1,则y=1﹣λ,z=
,令x=1,则y=1﹣λ,z= ![]() ,
,
平面PAB与平面PMQ所成锐二面角的大小为30°,
可得:cos30°= 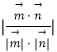 =
= 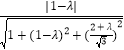 =
= ![]() ,
,
解得λ=3或 ![]() .
.
此时DQ=2在CD的延长线上,或DQ= ![]() 在CD线段上.
在CD线段上.
【解析】(1)在AD上取AN= ![]() AD,过N作NG∥DC,交AE于G,连结FG,FN,利用平面与平面平行的判定定理证明平面FNG∥平面PCD,推出FG∥平面PCD.(2)作PO⊥AB于O,BA所在直线为x轴,OP所在直线为z轴,在平面ABCD内作AB的垂线为y轴,求出平面PAB的法向量,平面PMQ的法向量,利用平面PAB与平面PMQ所成锐二面角的大小为30°,求解得λ推出CD的大小.
AD,过N作NG∥DC,交AE于G,连结FG,FN,利用平面与平面平行的判定定理证明平面FNG∥平面PCD,推出FG∥平面PCD.(2)作PO⊥AB于O,BA所在直线为x轴,OP所在直线为z轴,在平面ABCD内作AB的垂线为y轴,求出平面PAB的法向量,平面PMQ的法向量,利用平面PAB与平面PMQ所成锐二面角的大小为30°,求解得λ推出CD的大小.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

【题目】某设备的使用年数x与所支出的维修总费用y的统计数据如下表:
使用年数x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
根据上标可得回归直线方程为 ![]() =1.3x+
=1.3x+ ![]() ,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.
,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.