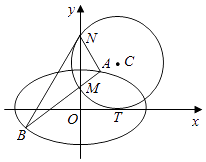题目内容
【题目】已知椭圆方程为![]() ,它的一个顶点为
,它的一个顶点为![]() ,离心率
,离心率![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
, ![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)椭圆的方程为![]() .(2)
.(2)![]() 面积取得最大值
面积取得最大值![]() .
.
【解析】试题分析:(1)由题意列关于a,b,c的方程组,求解可得a,b,c的值,则椭圆方程可求;
(2)当AB⊥x轴时, ![]() ;当AB与x轴不垂直时,设直线AB的方程为y=kx+m,由坐标原点O到直线l的距离为
;当AB与x轴不垂直时,设直线AB的方程为y=kx+m,由坐标原点O到直线l的距离为![]() 可得
可得![]() ,联立直线方程与椭圆方程,化为关于x的一元二次方程,由弦长公式求得|AB|,结合基本不等式求其最大值,则△AOB面积的最大值可求.
,联立直线方程与椭圆方程,化为关于x的一元二次方程,由弦长公式求得|AB|,结合基本不等式求其最大值,则△AOB面积的最大值可求.
试题解析:
(1)设![]() ,
,
依题意得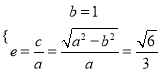 解得
解得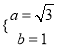 ∴椭圆的方程为
∴椭圆的方程为![]() .
.
(2)①当![]() 轴时,
轴时, ![]() .
.
②当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
由已知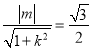 ,得
,得![]() ,把
,把![]() 代入椭圆方程,整理得
代入椭圆方程,整理得![]() ,
,
∴![]() .
.
∴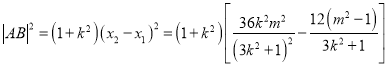 ,
,
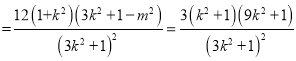
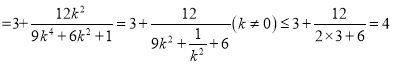 .
.
当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时![]() .③当
.③当![]() 时,
时, ![]() .综上所述:
.综上所述:
![]() ,此时
,此时![]() 面积取最大值
面积取最大值![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目