Question

【题目】数列{an}中，a1=2， （n∈N*）．
（1）证明数列 是等比数列，并求数列{an}的通项公式；
（2）设 ，若数列{bn}的前n项和是Tn ， 求证： ．

Answer 1

【答案】
（1）证明：数列{an}中，a1=2， （n∈N*），

= ，则数列 是首项为2，公比为 的等比数列；

则 =2（ ）n﹣1，

即为an=2n（ ）n﹣1

（2）解：证明： =

= ，

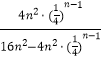
由2n=（1+1）n=1+n+ +…+ +1≥2n，

则4n≥4n2，

即有 ≤ = （ ﹣ ），

数列{bn}的前n项和是Tn= + + +…+

≤ （1﹣ + /span> ﹣ + ﹣ +…+ ﹣ ）

= （1﹣ ）＜ ，

则 ．

【解析】（1）将原式两边除以n+1，结合等比数列的定义和通项公式，即可得证；（2）求得 = ，可得4n≥4n2 ， 即有 ≤ = （ ﹣ ），运用数列的求和方法：裂项相消求和，结合不等式的性质，即可得证．
【考点精析】通过灵活运用等比数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：；数列{an}的前n项和sn与通项an的关系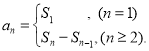即可以解答此题．