题目内容
16．不等式（$\frac{1}{2}$）${\;}^{2{x}^{2}-3x-9}$≤（$\frac{1}{2}$）${\;}^{{x}^{2}-8x-19}$的解集是（-∞，+∞）．分析 根据指数函数的单调性解指数不等式即可．
解答 解：∵（$\frac{1}{2}$）${\;}^{2{x}^{2}-3x-9}$≤（$\frac{1}{2}$）${\;}^{{x}^{2}-8x-19}$，
∴2x2-3x-9≥x2-8x-19，
即x2+5x+10≥0，
∵判别式△=25-40=-15＜0，
∴不等式的解集是（-∞，+∞），
故答案为：（-∞，+∞）
点评 本题主要考查不等式的求解，根据指数函数的单调性是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
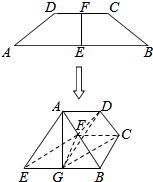在等腰梯形ABCD中，E，F分别是AB，CD的中点，AB=4，CD=2，AD=BC=$\sqrt{2}$，现将梯形AEFD沿EF折起，并记平面AEFD与平面BEFC所成二面角的平面角为θ，BE中点为G．