题目内容
定义:若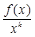 在
在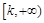 上为增函数,则称
上为增函数,则称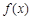 为“k次比增函数”,其中
为“k次比增函数”,其中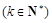 . 已知
. 已知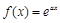 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若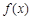 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当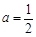 时,求函数
时,求函数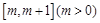 在
在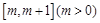 上的最小值;
上的最小值;
(3)求证: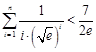 .
.
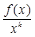 在
在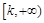 上为增函数,则称
上为增函数,则称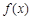 为“k次比增函数”,其中
为“k次比增函数”,其中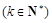 . 已知
. 已知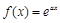 其中e为自然对数的底数.
其中e为自然对数的底数.(1)若
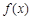 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;(2)当
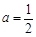 时,求函数
时,求函数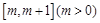 在
在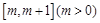 上的最小值;
上的最小值;(3)求证:
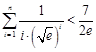 .
.(1)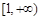 ;(2)详见解析;(3)详见解析.3.详见解析.
;(2)详见解析;(3)详见解析.3.详见解析.
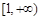 ;(2)详见解析;(3)详见解析.3.详见解析.
;(2)详见解析;(3)详见解析.3.详见解析.试题分析:(Ⅰ)由于
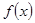 是“1次比增函数”,得到
是“1次比增函数”,得到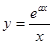 在
在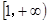 上为增函数,求导后,导数大于等于0,分离参数
上为增函数,求导后,导数大于等于0,分离参数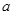 ,转化为恒成立,求最值的问题,即可得到实数a的取值范围;
,转化为恒成立,求最值的问题,即可得到实数a的取值范围;(Ⅱ)当
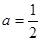 时,得到函数
时,得到函数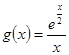 ,
,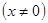 ,利用导数即可得到
,利用导数即可得到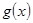 的单调区间,分成
的单调区间,分成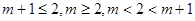 ,三种情况进行分类讨论即可函数在
,三种情况进行分类讨论即可函数在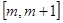
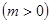 上单调性,进而得到其最小值;
上单调性,进而得到其最小值;(Ⅲ)由(Ⅱ)当
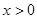 时,
时,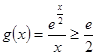 ,即
,即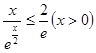 ,则
,则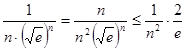 ,即可证明:
,即可证明: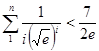 .,
.,试题解析:(1)由题意知
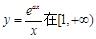 上为增函数,因为
上为增函数,因为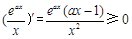 在
在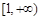 上
上恒成立.又
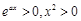 ,则
,则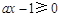 在
在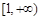 上恒成立,
上恒成立,即
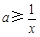 在
在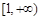 上恒成立. 而当
上恒成立. 而当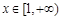 时,
时,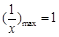 ,所以
,所以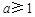 ,
,于是实数a的取值范围是
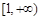 . 4分
. 4分(2)当
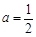 时,
时,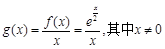 ,则
,则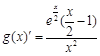 .
.当
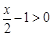 ,即
,即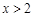 时,
时,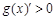 ;
;当
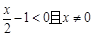 ,即
,即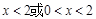 时,
时,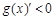 .
.则
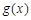 的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分
的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分因为
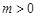 ,所以
,所以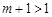 ,
,①当
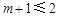 ,即
,即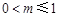 时,
时,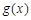 在[
在[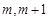 ]上单调递减,
]上单调递减,所以
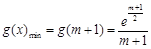 .
.②当
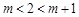 ,即
,即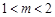 时,
时,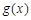 在
在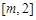 上单调递减,
上单调递减,在
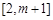 上单调递增,所以
上单调递增,所以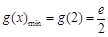 .
.③当
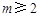 时,
时,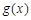 在[
在[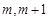 ]上单调递增,所以
]上单调递增,所以 .
.综上,当
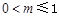 时,
时,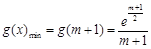 ;
;当
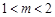 时,
时,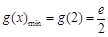 ;
;当
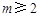 时,
时, . 9分
. 9分(3)由(2)可知,当
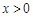 时,
时,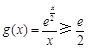 ,所以
,所以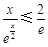
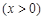 ,
,可得
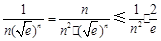 11分
11分于是
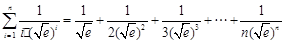
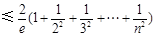
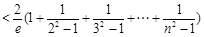
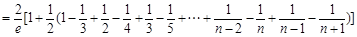

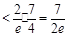 14分
14分
练习册系列答案
相关题目
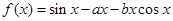
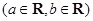 .
.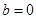 ,讨论函数
,讨论函数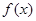 在区间
在区间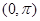 上的单调性;
上的单调性;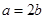 且
且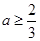 ,对任意的
,对任意的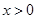 ,试比较
,试比较 的大小.
的大小.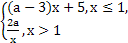 是(-∞,+∞)上的减函数,则a的取值范围是
是(-∞,+∞)上的减函数,则a的取值范围是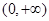 上单调递减,并且是偶函数的是( )
上单调递减,并且是偶函数的是( )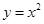
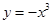
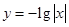
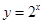
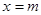 与函数
与函数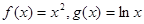 的图象分别交于点M、N,则|MN|的最小值为( )
的图象分别交于点M、N,则|MN|的最小值为( )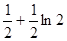
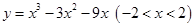 有( )
有( )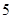 ,极小值
,极小值
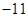
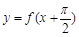 为定义在R上的偶函数,且当
为定义在R上的偶函数,且当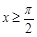 时,
时,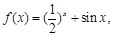 则下列选项正确的是( )
则下列选项正确的是( )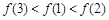
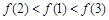
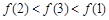
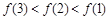
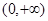 上的函数
上的函数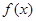 满足对任意的
满足对任意的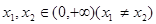 ,有
,有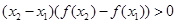 .则满足
.则满足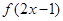 <
<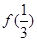 的x取值范围是( )
的x取值范围是( )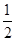 ,
,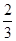 )
)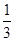 ,
,