题目内容
8.设函数f(x)的定义域为R,对任意x1,x2有f(x1)+f(x2)=2f($\frac{{x}_{1}+{x}_{2}}{2}$)•f($\frac{{x}_{1}-{x}_{2}}{2}$),且f($\frac{π}{2}$)=0,f(π)=-1.(1)求f(0)的值;
(2)求证:f(x)是偶函数,且f(π-x)=-f(x)
分析 (1)利用赋值法,令x1=x2=π,即可求f(0)的值;
(2)令x1=x,x2=-x,结合函数的奇偶性的定义进行证明即可.
解答 (1)令x1=x2=π,可得2f(π)=2f(π)f(0),
∵f(π)=-1,
∴得f(0)=1.
(2)令x1=x,x2=-x,可得f(x)+f(-x)=2f(x)•f(0)
∵f(0)=1∴f(x)=f(-x)
∴f(x)是偶函数;
令x1=π,x2=0,可得f(π)+f(0)=2f($\frac{π}{2}$)f($\frac{π}{2}$),
又∵f(0)=1,f(π)=-1,
∴f(0)+f(π)=0
∴得f($\frac{π}{2}$)=0,
令x1=x,x2=π-x,可得f(x)+f(π-x)=2f($\frac{π}{2}$)f($\frac{2x-π}{2}$)=0
∴f(π-x)+f(x)=0.
即f(π-x)=-f(x).
点评 本题主要考查抽象函数的应用,利用赋值法结合函数奇偶性的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.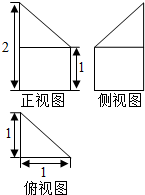 若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
 若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )| A. | $\frac{2}{3}$cm3 | B. | $\frac{1}{3}$cm3 | C. | 1cm3 | D. | 2cm3 |