题目内容
16.p为何值时,对任意实数x,不等式-9<$\frac{3{x}^{2}+px+6}{{x}^{2}-x+1}$≤6恒成立.分析 注意到所给的不等式分母为正,因此可以将问题转化为一元二次不等式恒成立问题,借助于二次函数的知识由判别式小于0,解二次不等式不难解决.
解答 解:不等式-9<$\frac{3{x}^{2}+px+6}{{x}^{2}-x+1}$≤6对?x∈R恒成立,
结合x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0恒成立,
故原式可化为12x2+(p-9)x+15>0且3x2-(p+1)x≥0对一切x∈R恒成立.
则只需△1=(p-9)2-4×12×15<0且△2=(p+1)2≤0.
则p+1=0,即p=-1.
即有p=-1时,原不等式恒成立.
点评 本题充分注意到分母大于零恒成立,从而将问题转化为一元二次不等式的恒成立问题是解题的关键.

练习册系列答案
相关题目
6.不等式$\frac{1+|x|}{|x|-1}$≥3的解集是( )
| A. | {x|-2≤x≤2} | B. | {x|-2≤x<-1或-1<x<1或1<x≤2} | ||
| C. | {x|x≤2且x≠±1} | D. | {x|-2≤x<-1或1<x≤2} |
7.(普通中学做)直线y=3x+2与曲线y=ax3+1相切,则实数a=( )
| A. | 4 | B. | 3 | C. | 2 | D. | -$\frac{1}{2}$ |
6.已知函数f(x)=2cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中($\frac{2}{3}$,y1)与($\frac{20}{3}$,y2)分别为函数f(x)图象的一个最高点和最低点,则函数(x)的一个单调增区间为( )
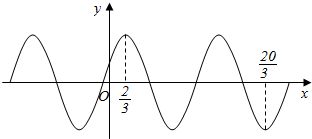

| A. | (-$\frac{16}{3}$,-$\frac{10}{3}$) | B. | (-$\frac{10}{3}$,0) | C. | (0,$\frac{4}{3}$) | D. | ($\frac{14}{3}$,$\frac{20}{3}$) |