题目内容

3．已知tan2α=2tan2β+1，证明：sin2β=2sin2α-1．

分析 把已知的等式化切函数为弦函数，然后结合平方关系得答案．

解答 证明：由tan2α=2tan2β+1，
得tan2α+1=2tan2β+2=2（tan2β+1），
即sec2α=2sec2β，
∴2cos2α=cos2β，
则2（1-sin2α）=1-sin2β，
∴sin2β=2sin2α-1．得证．

点评 本题考查了三角恒等式的证明，三角恒等式的证明掌握的原则是由繁到简，切割化弦，是基础题．

练习册系列答案
相关题目
13．已知甲、乙、丙、丁四位同学，在某个时段内每人互不重复地从语文、数学、英语、文综这四个科目中选择一科进行复习．现有下面五种均为正确的说法：
A．甲不在复习语文，也不在复习数学；B．乙不在复习英语，也不在复习语文；
C．丙不在复习文综，也不在复习英语；D．丁不在复习数学，也不在复习语文；
E．如果甲不在复习英语，那么丙不在复习语文．
根据以上信息，某同学判断如下：
①甲在复习英语  ②乙在复习文综  ③丙在复习数学  ④丁在复习英语
则上述所有判断正确的序号是④．
14．已知函数f（x）=x2-cosx，则f（$\frac{3}{5}$），f（0），f（-$\frac{1}{2}$）的大小关系．
11．已知数列{an}满足a1=$\frac{1}{3}$，a2=$\frac{7}{9}$，an+2=$\frac{4}{3}$an+1-$\frac{1}{3}$an（n∈N*）．
（1）求数列{an}的通项公式；
（2）求数列{nan}的前n项和Sn．
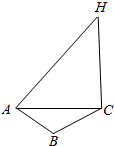18．为了测量音乐广场上喷泉的喷射最大高度，小明和小军一个站在A处，一个站在B处，喷泉的喷头在C处，且A、B、C三处位于同一水平面上，A、B两地相距20米，∠BAC=60°，经测量知AC的距离比BC的距离多5m，在A地测得该喷泉射的最高点H的仰角为45°，求该喷泉的最大垂直喷射高度CH．
8．设函数f（x）的定义域为R，对任意x1，x2有f（x1）+f（x2）=2f（$\frac{{x}_{1}+{x}_{2}}{2}$）•f（$\frac{{x}_{1}-{x}_{2}}{2}$），且f（$\frac{π}{2}$）=0，f（π）=-1．
（1）求f（0）的值；
（2）求证：f（x）是偶函数，且f（π-x）=-f（x）
15．在等比数列{an}中，已知a1+a3=20，a4+a6=$\frac{5}{2}$，求S5．
12．已知集合A={1，0，a}，若a2∈A，求实数a的值．
13．求证：在二次函数f（x）=ax2+bx+x中，若x1≠x2，则使“f（$\frac{{x}_{1}+{x}_{2}}{2}$）＜$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$成立”的充要条件是“a＞0”

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网