题目内容
17．
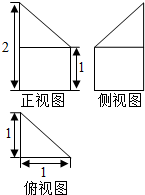若某多面体的三视图（单位：cm）如图所示，则此多面体的体积是（ ）| A． | $\frac{2}{3}$cm3 | B． | $\frac{1}{3}$cm3 | C． | 1cm3 | D． | 2cm3 |
分析 由已知中的三视图，可得该几何体由一个以俯视图为底面的三棱锥和三棱柱组成而成，分别求出他们的体积，相加可得答案．
解答 解：由已知中的三视图，可得该几何体由一个以俯视图为底面的三棱锥和三棱柱组成而成，
底面面积S=$\frac{1}{2}$×1×1=$\frac{1}{2}$cm2，
棱锥的高为2-1=1cm，棱柱的高为1cm，
故棱锥的体积为$\frac{1}{3}$×$\frac{1}{2}$×1=$\frac{1}{6}$cm3，棱柱的体积为：$\frac{1}{2}$×1=$\frac{1}{2}$cm3，
故组合体的体积V=$\frac{1}{6}$+$\frac{1}{2}$=$\frac{2}{3}$cm3，
故选：A．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
优生乐园系列答案
相关题目
7．（普通中学做）直线y=3x+2与曲线y=ax3+1相切，则实数a=（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | -$\frac{1}{2}$ |
6．已知函数f（x）=2cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中（$\frac{2}{3}$，y1）与（$\frac{20}{3}$，y2）分别为函数f（x）图象的一个最高点和最低点，则函数（x）的一个单调增区间为（ ）
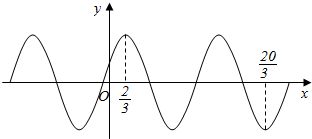
| A． | （-$\frac{16}{3}$，-$\frac{10}{3}$） | B． | （-$\frac{10}{3}$，0） | C． | （0，$\frac{4}{3}$） | D． | （$\frac{14}{3}$，$\frac{20}{3}$） |