题目内容
18．函数f（x）=-x2（x＞1）的反函数，f-1（x）=$\sqrt{-x}$，（x＜-1）．分析 由y=f（x）=-x2（x＞1），解得x=$\sqrt{-y}$（y＜-1），把x与y互换即可得出．
解答 解：由y=f（x）=-x2（x＞1），解得x=$\sqrt{-y}$（y＜-1），
把x与y互换可得y=$\sqrt{-x}$，（x＜-1）．
∴函数f（x）=-x2（x＞1）的反函数是f-1（x）=$\sqrt{-x}$，（x＜-1），
故答案为：$\sqrt{-x}$，（x＜-1）
点评 本题考查了反函数的求法，难度不大，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
6．已知函数f（x）=2cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中（$\frac{2}{3}$，y1）与（$\frac{20}{3}$，y2）分别为函数f（x）图象的一个最高点和最低点，则函数（x）的一个单调增区间为（ ）
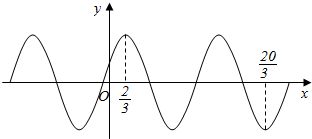
| A． | （-$\frac{16}{3}$，-$\frac{10}{3}$） | B． | （-$\frac{10}{3}$，0） | C． | （0，$\frac{4}{3}$） | D． | （$\frac{14}{3}$，$\frac{20}{3}$） |