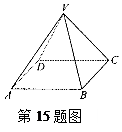
题目内容
如图,正四面体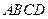 的顶点
的顶点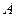 、
、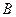 、
、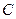 分别在两两垂直的三条射线
分别在两两垂直的三条射线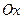 、
、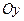 、
、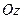 上,给出下列四个命题:
上,给出下列四个命题:
①多面体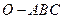 是正三棱锥;
是正三棱锥;
②直线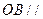 平面
平面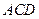 ;
;
③直线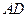 与
与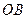 所成的角为
所成的角为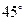 ;
;
④二面角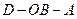 为
为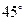 .
.
其中真命题有_______________(写出所有真命题的序号).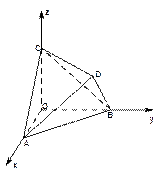
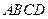 的顶点
的顶点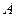 、
、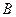 、
、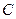 分别在两两垂直的三条射线
分别在两两垂直的三条射线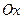 、
、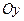 、
、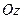 上,给出下列四个命题:
上,给出下列四个命题: ①多面体
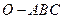 是正三棱锥;
是正三棱锥;②直线
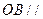 平面
平面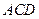 ;
;③直线
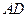 与
与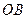 所成的角为
所成的角为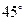 ;
; ④二面角
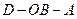 为
为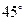 .
.其中真命题有_______________(写出所有真命题的序号).

①③④
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB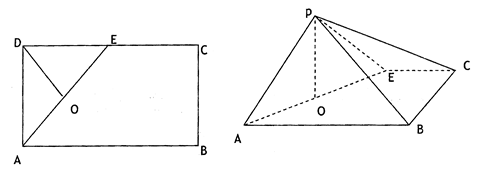 (1)求证:PO⊥面ABCE;
(1)求证:PO⊥面ABCE;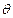 的正弦值.
的正弦值.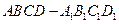 中,
中,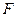 为
为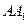 的中点,求证:
的中点,求证: 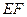 ∥面
∥面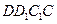 ;
;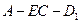 的余弦值;
的余弦值;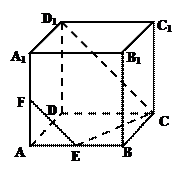
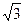 .
.

 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点. D所成角的正弦值;
D所成角的正弦值; 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
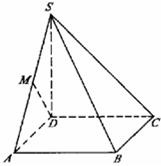
的值;若不存在,请说明理由。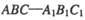 中,AC=BC=1, AAi="3"
中,AC=BC=1, AAi="3"  D为CCi上的点,二面角A-A1B-D的余弦值为
D为CCi上的点,二面角A-A1B-D的余弦值为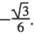
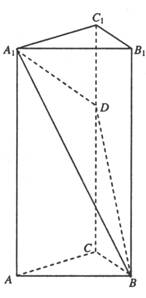
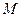 是棱
是棱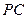 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: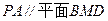 ;
;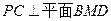 ;
;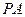 与直线
与直线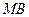 所成角的余弦值.
所成角的余弦值.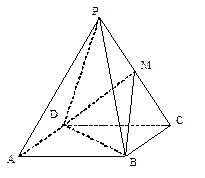

 的等腰三角形,则二面角V―AB―C的度数是 。
的等腰三角形,则二面角V―AB―C的度数是 。