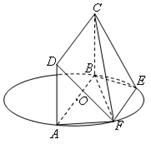
题目内容
(本小题满分12分)
如图,直三棱柱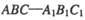 中,AC=BC=1, AAi="3"
中,AC=BC=1, AAi="3"  D为CCi上的点,二面角A-A1B-D的余弦值为
D为CCi上的点,二面角A-A1B-D的余弦值为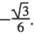
(I )求证:CD=2;
(II)求点A到平面A1BD的距离.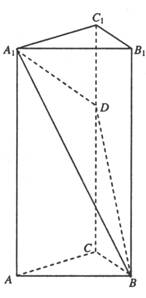
如图,直三棱柱
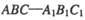 中,AC=BC=1, AAi="3"
中,AC=BC=1, AAi="3"  D为CCi上的点,二面角A-A1B-D的余弦值为
D为CCi上的点,二面角A-A1B-D的余弦值为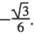
(I )求证:CD=2;
(II)求点A到平面A1BD的距离.

(Ⅰ)取AB中点E,A1B1中点G,连结EG,交A1B于F,连结CE、C1G,作DM⊥GE于M.
∵平面C1GEC⊥平面A1ABB1,∴DM⊥平面A1ABB1.
作MN⊥A1B于N,连结DN,则MN为DN在平面A1ABB1上的射影,则∠DNM为二面角B1-A1B-D的平面角.……………………………………………………………4分
∴cos∠DNM=,DM=C1G=,∴MN=.
∵sin∠MFN==,∴MF=,∴DC=2.…………………………7分
(Ⅱ)在△A1BD中,A1D=,BD=,A1B=.
cos∠A1DB==-,sin∠A1DB=,
S△A1BD=A1D·BDsin∠A1DB=,
又S△A1AB=××3=,点D到面A1AB的距离DM=CE=,
设点A到平面A1BD的距离为d,则
S△A1BD·d=S△A1AB×,∴d=.
故点A到平面A1BD的距离为.………………………………………………12分
∵平面C1GEC⊥平面A1ABB1,∴DM⊥平面A1ABB1.
作MN⊥A1B于N,连结DN,则MN为DN在平面A1ABB1上的射影,则∠DNM为二面角B1-A1B-D的平面角.……………………………………………………………4分
∴cos∠DNM=,DM=C1G=,∴MN=.
∵sin∠MFN==,∴MF=,∴DC=2.…………………………7分
(Ⅱ)在△A1BD中,A1D=,BD=,A1B=.
cos∠A1DB==-,sin∠A1DB=,
S△A1BD=A1D·BDsin∠A1DB=,
又S△A1AB=××3=,点D到面A1AB的距离DM=CE=,
设点A到平面A1BD的距离为d,则
S△A1BD·d=S△A1AB×,∴d=.
故点A到平面A1BD的距离为.………………………………………………12分
略

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 中,
中, ,
,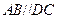 ,
,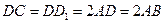
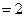 .
.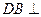 平面
平面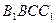 ;
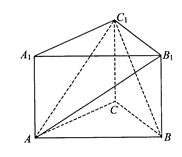
;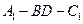 的余弦值.
的余弦值.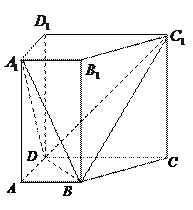
 中,
中, 垂直平分
垂直平分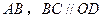 ,且
,且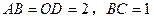 ,现将四边形
,现将四边形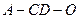 的正弦值;
的正弦值;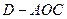 的体积。
的体积。
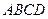 与
与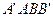 都是边长为
都是边长为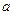 的正方形,点E是
的正方形,点E是 的中点,
的中点,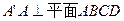
 平面BDE;
平面BDE; ⊥平面BDE
⊥平面BDE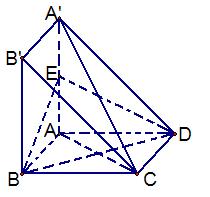
 中,底面
中,底面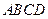 四边长为1的菱形,
四边长为1的菱形,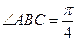 ,
,  ,
,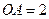 ,
,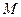 为
为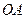 的中点,
的中点,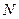 为
为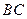 的中点
的中点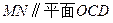 ;
;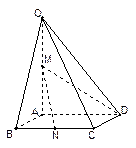
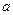 的正方体
的正方体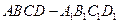 中,
中,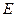 是线段
是线段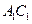 中点,
中点,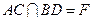 .
.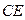 ^
^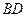 ;(Ⅱ) 求证:
;(Ⅱ) 求证: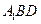 ;
;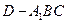 的体积.
的体积.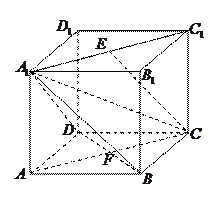
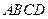 的顶点
的顶点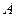 、
、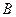 、
、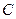 分别在两两垂直的三条射线
分别在两两垂直的三条射线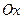 、
、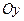 、
、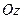 上,给出下列四个命题:
上,给出下列四个命题: 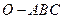 是正三棱锥;
是正三棱锥;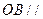 平面
平面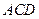 ;
;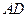 与
与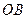 所成的角为
所成的角为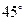 ;
; 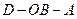 为
为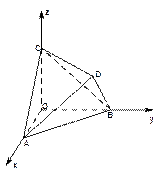
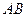 为圆
为圆 的直径,点
的直径,点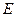 、
、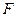 在圆
在圆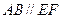 ,矩形
,矩形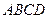 所在平面和圆
所在平面和圆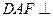 平面
平面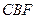 ;
;