题目内容
【题目】已知函数![]() .
.
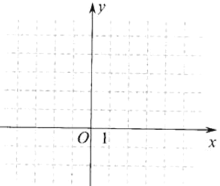
(1)设在平面直角坐标系中作出![]() 的图象,并写出不等式
的图象,并写出不等式![]() 的解集
的解集![]() .
.
(2)设函数![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)函数图象如下图:
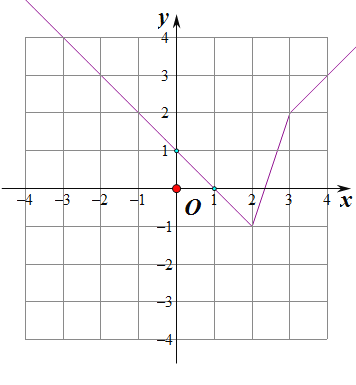
不等式![]() 的解集
的解集![]() ;
;
(2)![]() .
.
【解析】
(1)利用零点法化简函数的解析式,在直角坐标系内,画出函数图象,分类讨论解不等式;
(2)根据(1)对![]() 时,进行分类讨论:
时,进行分类讨论:
当![]() 时,
时,![]() ,根据
,根据![]() 取值的不同范围,利用一次函数的单调性,求出
取值的不同范围,利用一次函数的单调性,求出![]() 的取值范围;
的取值范围;
当![]() 时,
时,![]() ,根据
,根据![]() 取值的不同范围,利用一次函数的单调性,求出
取值的不同范围,利用一次函数的单调性,求出![]() 的取值范围,最后确定
的取值范围,最后确定![]() 的取值范围.
的取值范围.
(1)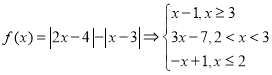 ,画出图象,如下图所示:
,画出图象,如下图所示:

当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,所以
,所以
不等式![]() 的解集
的解集![]() .
.
(2)当![]() 时,
时,![]()
当![]() 时,
时,![]() ,显然成立;
,显然成立;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() 即可,也就是
即可,也就是
![]() ;
;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() ,
,
所以当![]() 时,当
时,当![]() ,
,![]() 的取值范围
的取值范围![]() ;
;
当![]() 时,
时,![]() ,
,
当![]() 时,显然
时,显然![]() 不成立;
不成立;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() 不存在这样的
不存在这样的![]() ;
;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() ,
,
所以当![]() 时,当
时,当![]() ,
,![]() 的取值范围是
的取值范围是![]() ,
,
综上所述![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
相关题目