题目内容
【题目】已知椭圆
的离心率为
，与
轴交于点
，
，过轴上一点
引轴的垂线，交椭圆
于点
，
，当与椭圆右焦点重合时，
．
（1）求椭圆的方程；
（2）设直线
与直线
交于点
，是否存在定点
和
，使
为定值．若存在，求、点的坐标；若不存在，说明理由．
【答案】（1）
（2）存在，
为
，
．
【解析】
（1）
是椭圆的通径，由此已知条件可表示为
的两个等式，结合
可求得
，得椭圆方程；
（2）设
点坐标为
，
，
，不妨设
，
．在直线
可得
的关系，同理由在直线
又得一关系式，消去
可得点轨迹方程，轨迹是双曲线，由双曲线定义可作答．
（1）由题知：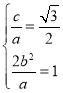
，解得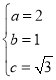
，
故椭圆
的方程为．
（2）设点坐标为，，，
不妨设，．
则，
，
三点共线，
，①
同理：
，②
得：
，
又在椭圆上，
，
代入整理得：
．
即点的轨迹为双曲线
，
取、
为该双曲线的左、右焦点．
即
，．
此时
为定值，故为，．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
