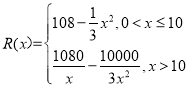题目内容
【题目】设函数f（x）＝|x﹣2|+|x+1|．
（1）解不等式f（x）≥4．
（2）若f（x）+f（y）≤6，求x+y的取值范围．
【答案】（1）
；（2）[﹣2，4]．
【解析】
（1）分类讨论去绝对值，转化解一元一次不等式组；
（2）根据绝对值不等式的性质，求出f（x）+f（y）的最小值，结合已知可求出f（x）+f（y）的值，进而求出结论.
（1）f（x）＝|x﹣2|+|x+1|
．
∵f（x）≥4，∴
或
，
∴
或
，
∴不等式的解集为；
（2）f（x）+f（y）＝|x﹣2|+|x+1|+|y﹣2|+|y+1|
≥|x+y﹣4|+|x+y+2|≥|（x+y﹣4）﹣（x+y+2）|＝6，
当且仅当（x+y﹣4）（x+y+2）≤0，即﹣2≤x+y≤4时取等号，
∵f（x）+f（y）≤6，∴|x+y﹣4|+|x+y+2|≤6，
∴|x+y﹣4|+|x+y+2|＝6，∴﹣2≤x+y≤4，
∴x+y的取值范围为[﹣2，4]．
【题目】中国北京世界园艺博览会于2019年4月29日至10月7日在北京市延庆区举行．组委会为方便游客游园，特推出“导引员”服务．“导引员”的日工资方案如下：
方案：由三部分组成
（表一）
底薪 | 150元 |
工作时间 | 6元/小时 |
行走路程 | 11元/公里 |
方案：由两部分组成：（1）根据工作时间20元/小时计费；（2）行走路程不超过4公里时，按10元/公里计费；超过4公里时，超出部分按15元/公里计费．已知“导引员”每天上班8小时，由于各种因素，“导引员”每天行走的路程是一个随机变量．试运行期间，组委会对某天100名“导引员”的行走路程述行了统计，为了计算方便对日行走路程进行取整处理．例如行走1.8公里按1公里计算，行走5.7公里按5公里计算．如表所示：
（表二）
行走路程 （公里） |
|
|
|
|
|
人数 | 5 | 10 | 15 | 45 | 25 |
（Ⅰ）分别写出两种方案的日工资
（单位：元）与日行走路程
（单位：公里）
的函数关系
（Ⅱ）①现按照分层抽样的方工式从
，
共抽取5人组成爱心服务队，再从这5人中抽取3人当小红帽，求小红帽中恰有1人来自的概率；
②“导引员”小张因为身体原因每天只能行走12公里，如果仅从日工资的角度考虑，请你帮小张选择使用哪种方案会使他的日工资更高？
