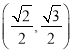题目内容
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 是抛物线
是抛物线![]() 上不同两点,且
上不同两点,且![]() (其中
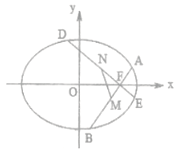
(其中![]() 是坐标原点),直线
是坐标原点),直线![]() 与
与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求抛物线![]() 的准线方程;
的准线方程;
(Ⅱ)求证:直线![]() 与
与![]() 轴平行.
轴平行.
【答案】(1) ![]() .(2)见解析.
.(2)见解析.
【解析】
(Ⅰ)把点代入即可求出p的值,可得抛物线C的准线方程,
(Ⅱ)由题意可设直线AB的方程为y=x+m,设A(x1,y1),B(x2,y2),由题意可得y1+y2=2,即可求出点Q的纵坐标,再分别求出直线OA,BM的方程,求出点P的纵坐标,即可证明.
(Ⅰ)由题意得![]() ,解得
,解得![]() .
.
所以抛物线![]() 的准线方程为
的准线方程为![]() .
.
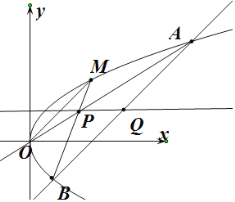
(Ⅱ)设![]() ,
,![]() ,
,
由![]() 得
得![]() ,则
,则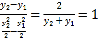 ,所以
,所以![]() .
.
所以线段![]() 中点
中点![]() 的为纵坐标
的为纵坐标![]() .
.
直线![]() 方程为
方程为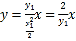 ┅①
┅①
直线![]() 方程为
方程为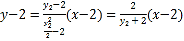 ┅②
┅②
联立①②解得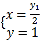 ,即点
,即点![]() 的为纵坐标
的为纵坐标![]() .
.
如果直线![]() 斜率不存在,结论也显然成立.
斜率不存在,结论也显然成立.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某工厂的机器上存在一种易损元件,这种元件发生损坏时,需要及时维修. 现有甲、乙两名工人同时从事这项工作,下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
甲维修的元件数 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
乙维修的元件数 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
(1)从这![]() 天中,随机选取一天,求甲维修的元件数不少于5件的概率;
天中,随机选取一天,求甲维修的元件数不少于5件的概率;
(2)试比较这10天中甲维修的元件数的方差![]() 与乙维修的元件数的方差
与乙维修的元件数的方差![]() 的大小.(只需写出结论);
的大小.(只需写出结论);
(3)由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加几名工人.
【题目】十八大以来,我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源产品年销售 | 1.6 | 6.2 | 17.7 | 33.1 | 55.6 |
(1)请画出上表中年份代码![]() 与年销量
与年销量![]() 的数据对应的散点图,并根据散点图判断.
的数据对应的散点图,并根据散点图判断.
![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年份代码
关于年份代码![]() 的回归方程类型;
的回归方程类型;
(2)根据(Ⅰ)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
参考公式: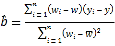 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:
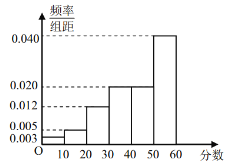
经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体,假设这两个项目的测试成绩相互独立.
(i)从该市测试人员中随机抽取1人,估计其“文化项目等级高于经济项目等级”的概率.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.