题目内容
4. 某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185) | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
分析 (1)根据频率、频数与样本容量的关系,求出对应的数值,画出频率分布直方图;
(2)利用分层抽样原理,求出各小组应抽取的人数;
(3)利用列举法求出基本事件数,计算对应的概率值.
解答 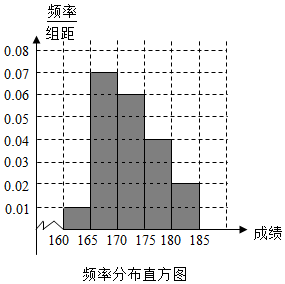 解:(1)由题可知,第2组的频数为0.35×100=35人,
解:(1)由题可知,第2组的频数为0.35×100=35人,
第3组的频率为$\frac{30}{100}$=0.300,频率分布直方图如图所示;
(2)因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:$\frac{30}{60}$×6=3人;第4组:$\frac{20}{60}$×6=2人;
第5组:$\frac{10}{60}$×6=1人.
所以第3、4、5组分别抽取3人、2人、1人.
(3)设第3组的3位同学为A1、A2、A3,
第4组的2位同学为B1、B2,第5组的1位同学为C,
则从六位同学中抽两位同学有15种可能,具体如下:
A1A2,A1A3,A1B1,A1B2,A1C,A2A3,
A2B1,A2B2,A2C,A3B1,A3B2,A3C,B1B2,B1C,B2C;
其中第4组的2位同学B1,B2至少有一位同学入选的有:
A1B1,A1B2,A2B1,A2B2,A3B1,A3B2,B1B2,B1C,B2C共9种可能;
所以其中第4组的2位同学B1、B2至少有一位同学入选的概率为
P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,考查了利用列举法求概率的应用问题,是基础题目.

练习册系列答案
相关题目
9.“已知关于x的不等式ax2+bx+c>0的解集为(1,2),解关于x的不等式cx2+bx+a>0.”给出如下的一种解法:
解:由ax2+bx+c>0的解集为(1,2),得,a($\frac{1}{x}$)2+b($\frac{1}{x}$)+c>0的解集为($\frac{1}{2}$,1),
即关于x的不等式cx2+bx+a>0的解集为($\frac{1}{2}$,1).
参考上述解法:若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$<0的解集为(-1,-$\frac{1}{3}$)∪($\frac{1}{2}$,1),则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$>0的解集为( )
解:由ax2+bx+c>0的解集为(1,2),得,a($\frac{1}{x}$)2+b($\frac{1}{x}$)+c>0的解集为($\frac{1}{2}$,1),
即关于x的不等式cx2+bx+a>0的解集为($\frac{1}{2}$,1).
参考上述解法:若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$<0的解集为(-1,-$\frac{1}{3}$)∪($\frac{1}{2}$,1),则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$>0的解集为( )
| A. | (-1,1) | B. | (-1,-$\frac{1}{2}$)∪($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,1) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,+∞) |
13.已知命题p:函数y=f(x)在区间[a,b]上单调递增,命题q:函数y=f(x)单调递增区间为[a,b],则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
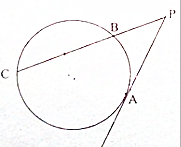 如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.
如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.