题目内容
【题目】已知椭圆C: ![]() ,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2. 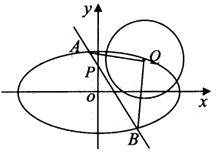
(1)求椭圆C的方程;
(2)过点P作直线l交椭圆C于A,B两点,若S△AQB=tan∠AQB,求直线l的方程.
【答案】
(1)解:因为椭圆C的右焦点F(c,0),|PF|=2,所以 ![]() ,
,
因为Q(2,1)在椭圆C上,所以 ![]() ,
,
由a2﹣b2=3,得a2=6,b2=3,
所以椭圆C的方程为 ![]()
(2)解:由S△AQB=tan∠AQB得: ![]() ,
,
即QAQBcos∠AQB=2,可得 ![]() ,
,
① 当l垂直x轴时, ![]()
![]() ,
,
此时满足题意,所以此时直线l的方程为x=0;
②当l不垂直x轴时,设直线l的方程为y=kx+1,
由 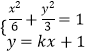 消去y得(1+2k2)x2+4kx﹣4=0,
消去y得(1+2k2)x2+4kx﹣4=0,
设A(x1,y1),B(x2,y2),所以 ![]() ,
, ![]() ,
,
代入 ![]() 可得:(x1﹣2,y1﹣1)(x2﹣2,y2﹣1)=2,
可得:(x1﹣2,y1﹣1)(x2﹣2,y2﹣1)=2,
代入y1=kx1+1,y2=kx2+1,得 ![]() ,
,
代入化简得: ![]() ,解得
,解得 ![]() ,
,
经检验满足题意,则直线l的方程为x﹣4y+4=0,
综上所述直线l的方程为x=0或x﹣4y+4=0
【解析】(1)由点P(0,1)到椭圆C的右焦点的距离为2PF|=2,可得c,由Q(2,1)在椭圆C上,得 ![]() ,及a2﹣b2=3,得a2 , b2 , (2)由S△AQB=tan∠AQB得:
,及a2﹣b2=3,得a2 , b2 , (2)由S△AQB=tan∠AQB得: ![]() ,即QAQBcos∠AQB=2,可得
,即QAQBcos∠AQB=2,可得 ![]() ,再联立直线与椭圆方程,由韦达定理可求解.
,再联立直线与椭圆方程,由韦达定理可求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目