题目内容
【题目】已知函数f（x）=|x|+|x﹣4|，则不等式f（x2+2）＞f（x）的解集用区间表示为 ．
【答案】
【解析】解：令g（x）=f（x2+2）﹣f（x）=x2+2+|x2﹣2|﹣|x|﹣|x﹣4|， x≥4时，g（x）=2x2﹣2x+4＞0，解得：x≥4；
≤x＜4时，g（x）=2x2﹣4＞0，解得：x＞ 或x＜﹣ ，
故 ＜x＜4；
0≤x＜ 时，g（x）=0＞0，不合题意；
﹣ ≤x＜0时，g（x）=2x＞0，不合题意；
x＜﹣ 时，g（x）=2x2+2x﹣4＞0，解得：x＞1或x＜﹣2，
故x＜﹣2，
所以答案是： ．
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能正确解答此题．
练习册系列答案
相关题目
【题目】已知函数 
（ 
），若函数F（x）=f（x）﹣3的所有零点依次记为x1 ， x2 ， x3 ， …，xn ， 且x1＜x2＜x3＜…＜xn ， 则x1+2x2+2x3+…+2xn﹣1+xn= ．
【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：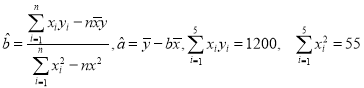
.