题目内容
【题目】Sn表示等差数列{an}的前n项的和，且S4=S9 ， a1=﹣12
（1）求数列的通项an及Sn；
（2）求和Tn=|a1|+|a2|+…+|an|
【答案】
（1）解：∵S4=S9，a1=﹣12，
∴4×（﹣12）+6d=9×（﹣12）+36d
解得d=2
∴ 
（2）解：当n≤6时，an＜0，|an|=﹣an，
Tn=﹣（a1+a2+… 
=13n﹣n2，
当n≥7时，an≥0，
Tn=﹣（a1+a2+…+a6）+（a7+… 
=Sn﹣2（a1+a2+…+a6）
=n2﹣13n+84
【解析】（1）由已知结合等差数列前n项和公式，构造关于公差d的方程，求出公差后，可得数列的通项an及Sn；（2）由（1）中数列的通项公式，可得数列前6项为负，故可分n≤6和n≥7时两种情况，结合等差数列前n项和公式求Tn ．
【考点精析】认真审题，首先需要了解等差数列的前n项和公式(前n项和公式：
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系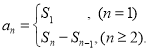
)的相关知识才是答题的关键．
练习册系列答案
相关题目
