Question

【题目】在四面体ABCD中，过棱AB的上一点E作平行于AD，BC的平面分别交四面体的棱BD，DC，CA于点F，G，H

（1）求证：截面EFGH为平行四边形

（2）若P、Q在线段BD、AC上，，且P、F不重合，证明：PQ∥截面EFGH

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）利用线面平行的性质定理得出线线平行，再利用平行公理得出又一组线线平行，有两组对边互相平行即可得证.

(2)先由题目中的比例证得两组线线平行，由面面平行的判定定理即可得证.

（1）证明：∵AD∥平面EFGH，平面ADB平面EHGH=EF，AD平面ABD，

∴AD∥EF ∵AD∥平面EHGH，平面ADC平面EHGH=GH，AD平面ADC，. ∴AD∥GH

由平行公理可得EF∥GH

同理可得EH∥FG

∴四边形EFGH为平行四边形.

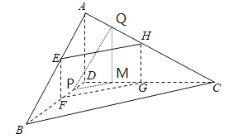
（2）如图在CD上取点M，使，连接MQ

则PM∥BC∥FG，，则QM∥AD∥HG

PMQM=M∴平面PMQ∥平面EHGH

∵PQ平面PMQ

∴PQ∥截面EFGH